Question Number 166917 by ajfour last updated on 02/Mar/22
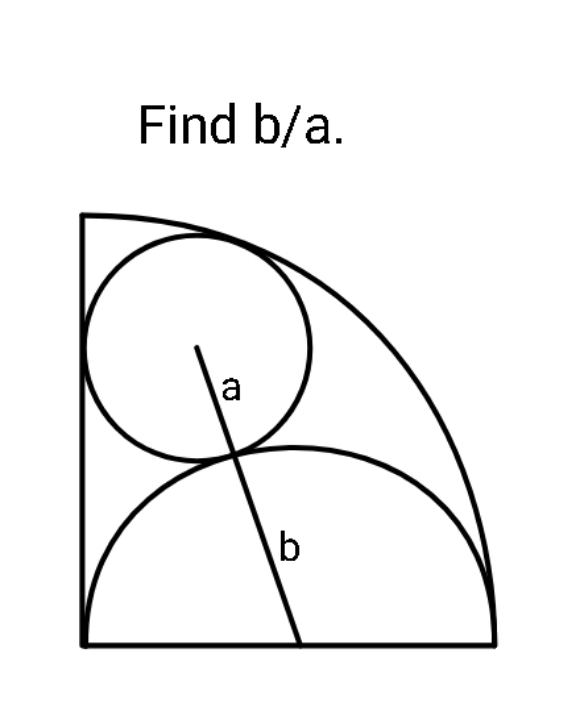
Commented by mr W last updated on 02/Mar/22
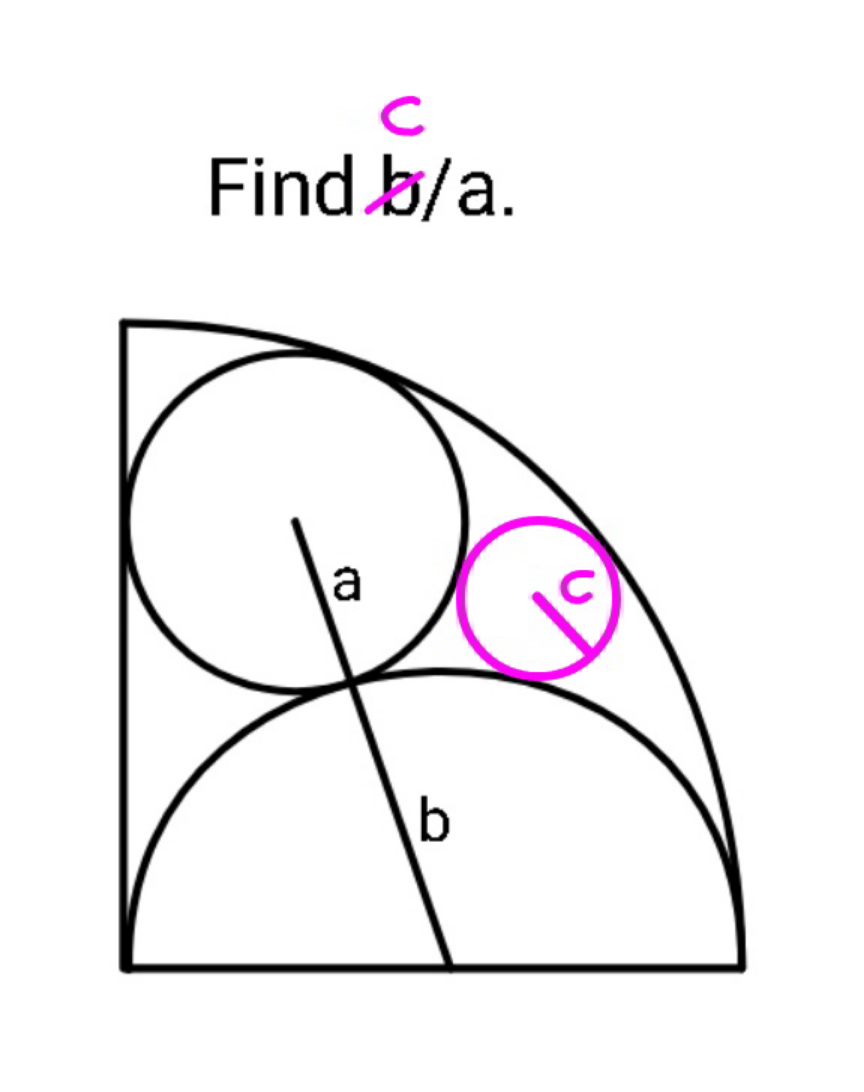
Commented by ajfour last updated on 02/Mar/22
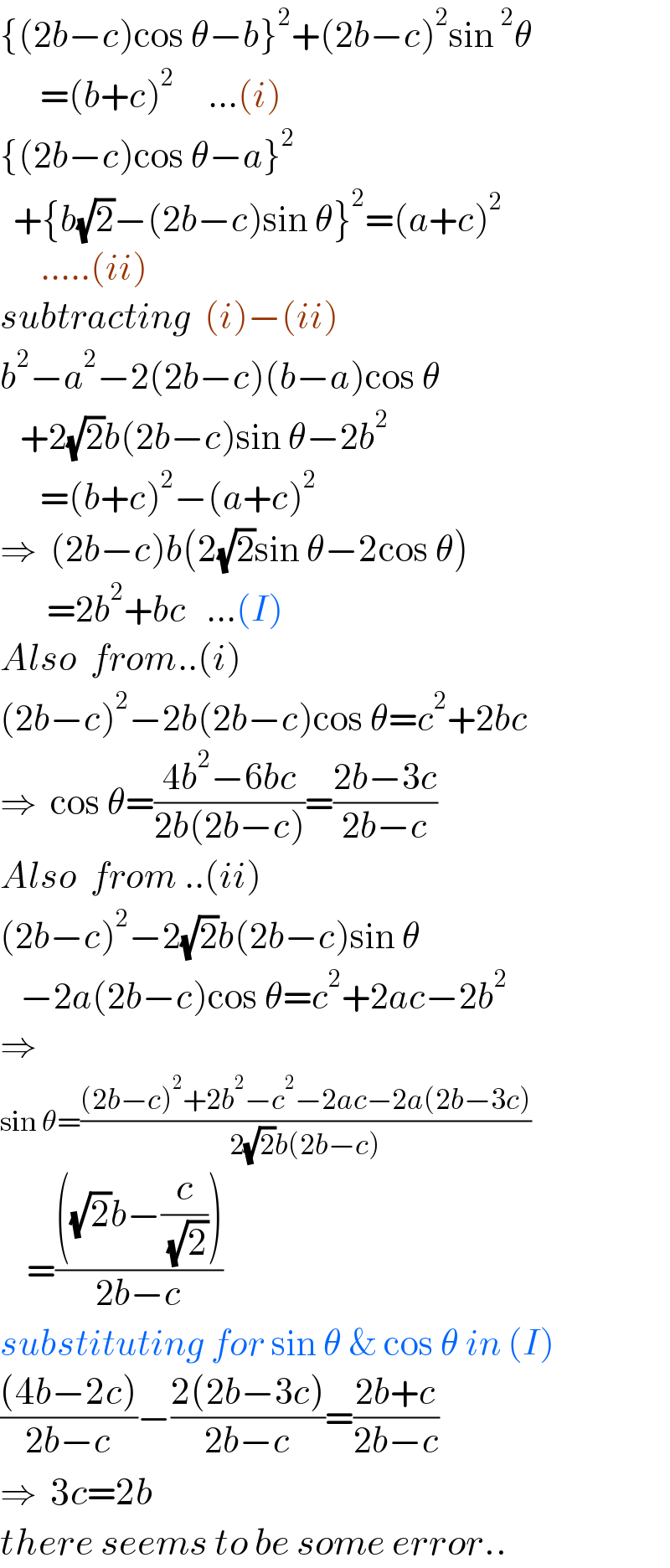
$$\left\{\left(\mathrm{2}{b}−{c}\right)\mathrm{cos}\:\theta−{b}\right\}^{\mathrm{2}} +\left(\mathrm{2}{b}−{c}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:=\left({b}+{c}\right)^{\mathrm{2}} \:\:\:\:\:…\left({i}\right) \\ $$$$\left\{\left(\mathrm{2}{b}−{c}\right)\mathrm{cos}\:\theta−{a}\right\}^{\mathrm{2}} \\ $$$$\:\:+\left\{{b}\sqrt{\mathrm{2}}−\left(\mathrm{2}{b}−{c}\right)\mathrm{sin}\:\theta\right\}^{\mathrm{2}} =\left({a}+{c}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:…..\left({ii}\right) \\ $$$${subtracting}\:\:\left({i}\right)−\left({ii}\right) \\ $$$${b}^{\mathrm{2}} −{a}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}{b}−{c}\right)\left({b}−{a}\right)\mathrm{cos}\:\theta \\ $$$$\:\:\:+\mathrm{2}\sqrt{\mathrm{2}}{b}\left(\mathrm{2}{b}−{c}\right)\mathrm{sin}\:\theta−\mathrm{2}{b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\left({b}+{c}\right)^{\mathrm{2}} −\left({a}+{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left(\mathrm{2}{b}−{c}\right){b}\left(\mathrm{2}\sqrt{\mathrm{2}}\mathrm{sin}\:\theta−\mathrm{2cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{2}{b}^{\mathrm{2}} +{bc}\:\:\:…\left({I}\right) \\ $$$${Also}\:\:{from}..\left({i}\right) \\ $$$$\left(\mathrm{2}{b}−{c}\right)^{\mathrm{2}} −\mathrm{2}{b}\left(\mathrm{2}{b}−{c}\right)\mathrm{cos}\:\theta={c}^{\mathrm{2}} +\mathrm{2}{bc} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\theta=\frac{\mathrm{4}{b}^{\mathrm{2}} −\mathrm{6}{bc}}{\mathrm{2}{b}\left(\mathrm{2}{b}−{c}\right)}=\frac{\mathrm{2}{b}−\mathrm{3}{c}}{\mathrm{2}{b}−{c}} \\ $$$${Also}\:\:{from}\:..\left({ii}\right) \\ $$$$\left(\mathrm{2}{b}−{c}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{b}\left(\mathrm{2}{b}−{c}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:−\mathrm{2}{a}\left(\mathrm{2}{b}−{c}\right)\mathrm{cos}\:\theta={c}^{\mathrm{2}} +\mathrm{2}{ac}−\mathrm{2}{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\: \\ $$$$\mathrm{sin}\:\theta=\frac{\left(\mathrm{2}{b}−{c}\right)^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} −{c}^{\mathrm{2}} −\mathrm{2}{ac}−\mathrm{2}{a}\left(\mathrm{2}{b}−\mathrm{3}{c}\right)}{\mathrm{2}\sqrt{\mathrm{2}}{b}\left(\mathrm{2}{b}−{c}\right)} \\ $$$$\:\:\:\:=\frac{\left(\sqrt{\mathrm{2}}{b}−\frac{{c}}{\:\sqrt{\mathrm{2}}}\right)}{\mathrm{2}{b}−{c}} \\ $$$${substituting}\:{for}\:\mathrm{sin}\:\theta\:\&\:\mathrm{cos}\:\theta\:{in}\:\left({I}\right) \\ $$$$\frac{\left(\mathrm{4}{b}−\mathrm{2}{c}\right)}{\mathrm{2}{b}−{c}}−\frac{\mathrm{2}\left(\mathrm{2}{b}−\mathrm{3}{c}\right)}{\mathrm{2}{b}−{c}}=\frac{\mathrm{2}{b}+{c}}{\mathrm{2}{b}−{c}} \\ $$$$\Rightarrow\:\:\mathrm{3}{c}=\mathrm{2}{b} \\ $$$${there}\:{seems}\:{to}\:{be}\:{some}\:{error}.. \\ $$
Commented by mr W last updated on 02/Mar/22

$${something}\:{seems}\:{wrong}\:{indeed}\:{sir}. \\ $$$${i}\:{got}\:{in}\:{an}\:{other}\:{way}\:\left({see}\:{Q}\mathrm{77681}\right): \\ $$$$\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{\mathrm{2}{a}}+\frac{\mathrm{1}}{{c}}−\frac{\mathrm{1}}{\mathrm{4}{a}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{16}{a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{17}\left(\frac{{c}}{{a}}\right)^{\mathrm{2}} −\mathrm{40}\left(\frac{{c}}{{a}}\right)+\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\frac{{c}}{{a}}=\frac{\mathrm{4}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{17}}\approx\mathrm{0}.\mathrm{511} \\ $$
Commented by Tawa11 last updated on 03/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 02/Mar/22
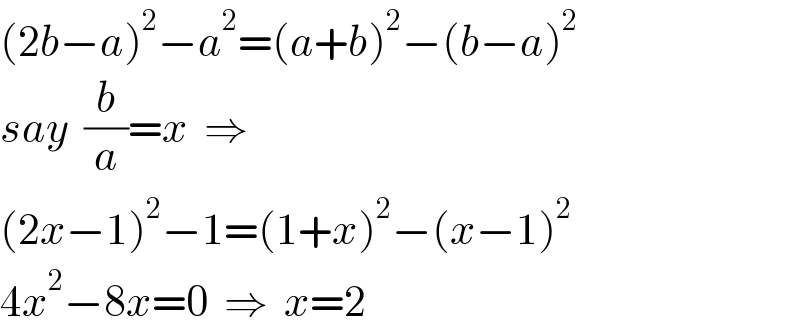
$$\left(\mathrm{2}{b}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} −\left({b}−{a}\right)^{\mathrm{2}} \\ $$$${say}\:\:\frac{{b}}{{a}}={x}\:\:\Rightarrow \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\left(\mathrm{1}+{x}\right)^{\mathrm{2}} −\left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{8}{x}=\mathrm{0}\:\:\Rightarrow\:\:{x}=\mathrm{2} \\ $$
Answered by cherokeesay last updated on 02/Mar/22
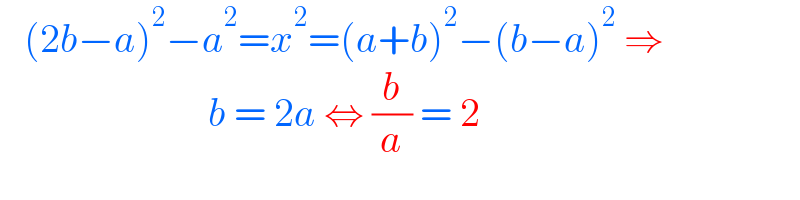
$$\:\:\:\left(\mathrm{2}{b}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} ={x}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} −\left({b}−{a}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}\:=\:\mathrm{2}{a}\:\Leftrightarrow\:\frac{{b}}{{a}}\:=\:\mathrm{2} \\ $$
