Question Number 166921 by cortano1 last updated on 02/Mar/22
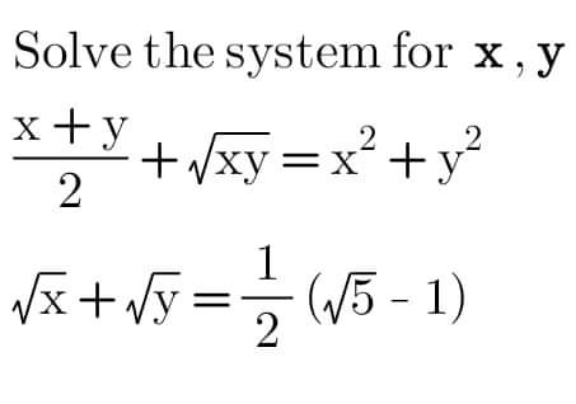
Commented by MJS_new last updated on 03/Mar/22
![(2) (√x)+(√y)=2u>0 [let u=(1/4)((√5)−1)] ⇒ (√x)=u−vi∧(√y)=u+vi∧u,v ∈R [we can let v≥0 because of symmetry] ⇒ (1) v^4 −6u^2 v^2 +u^2 (u^2 −1)=0 to get v≥0 only one solution fits: v=(√(3u^2 +u(√(8u^2 +1)))) now insert u=(1/4)((√5)−1) the exact values are possible to get but not very easy to handle... x≈.309016994375±.834799117309i y≈.309016994375∓.834799117309i](https://www.tinkutara.com/question/Q166937.png)
$$\left(\mathrm{2}\right) \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\mathrm{2}{u}>\mathrm{0}\:\left[\mathrm{let}\:{u}=\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\right] \\ $$$$\Rightarrow\:\sqrt{{x}}={u}−{v}\mathrm{i}\wedge\sqrt{{y}}={u}+{v}\mathrm{i}\wedge{u},{v}\:\in\mathbb{R} \\ $$$$\:\:\:\:\:\left[\mathrm{we}\:\mathrm{can}\:\mathrm{let}\:{v}\geqslant\mathrm{0}\:\mathrm{because}\:\mathrm{of}\:\mathrm{symmetry}\right] \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{1}\right) \\ $$$${v}^{\mathrm{4}} −\mathrm{6}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{u}^{\mathrm{2}} \left({u}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{to}\:\mathrm{get}\:{v}\geqslant\mathrm{0}\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{fits}: \\ $$$${v}=\sqrt{\mathrm{3}{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{8}{u}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{now}\:\mathrm{insert}\:{u}=\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right) \\ $$$$\mathrm{the}\:\mathrm{exact}\:\mathrm{values}\:\mathrm{are}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{get}\:\mathrm{but}\:\mathrm{not} \\ $$$$\mathrm{very}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{handle}… \\ $$$${x}\approx.\mathrm{309016994375}\pm.\mathrm{834799117309i} \\ $$$${y}\approx.\mathrm{309016994375}\mp.\mathrm{834799117309i} \\ $$
