Menu Close

Question-167010

Tinku Tara 0 Comments
Pin




Question Number 167010 by mnjuly1970 last updated on 04/Mar/22
Answered by LowLevelLump last updated on 04/Mar/22
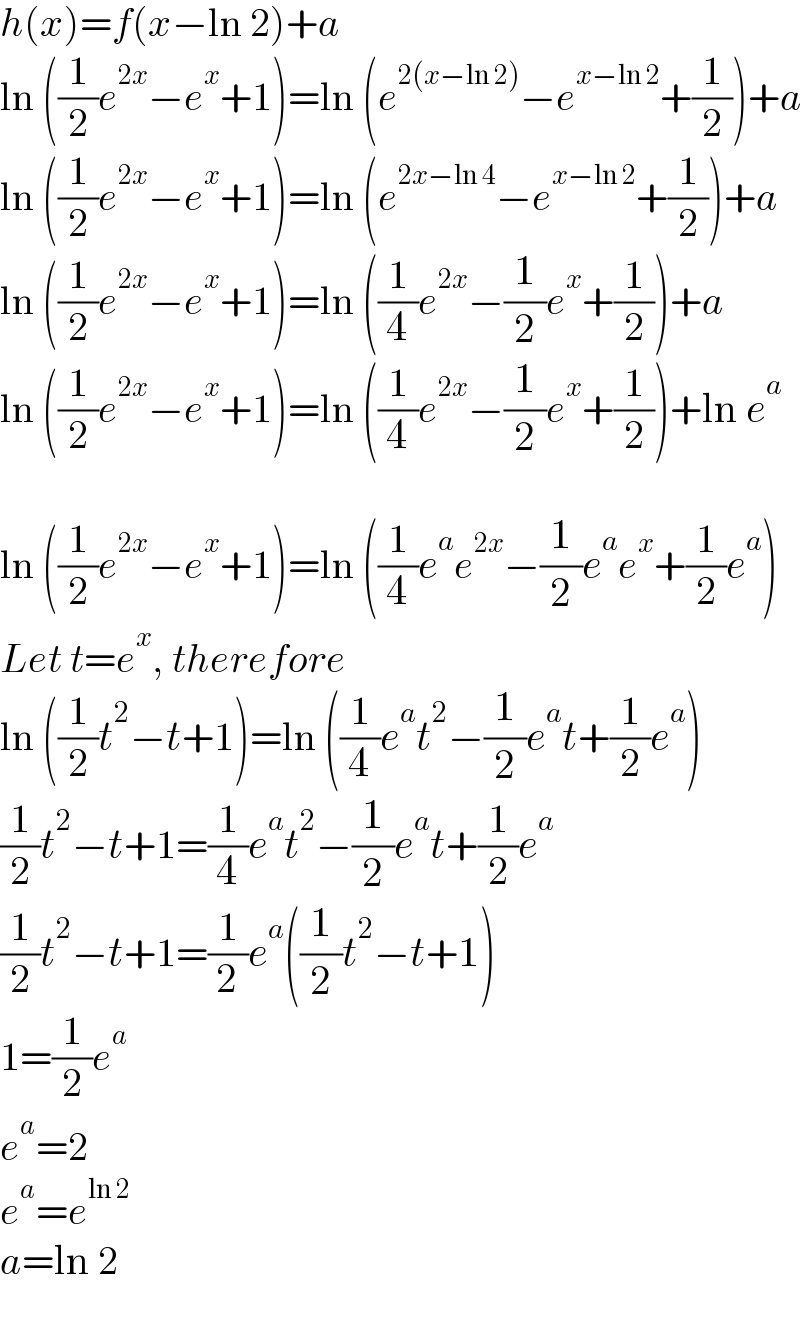
h(x)=f(x−ln 2)+a ln ((1/2)e^(2x) −e^x +1)=ln (e^(2(x−ln 2)) −e^(x−ln 2) +(1/2))+a ln ((1/2)e^(2x) −e^x +1)=ln (e^(2x−ln 4) −e^(x−ln 2) +(1/2))+a ln ((1/2)e^(2x) −e^x +1)=ln ((1/4)e^(2x) −(1/2)e^x +(1/2))+a ln ((1/2)e^(2x) −e^x +1)=ln ((1/4)e^(2x) −(1/2)e^x +(1/2))+ln e^a ln ((1/2)e^(2x) −e^x +1)=ln ((1/4)e^a e^(2x) −(1/2)e^a e^x +(1/2)e^a ) Let t=e^x , therefore ln ((1/2)t^2 −t+1)=ln ((1/4)e^a t^2 −(1/2)e^a t+(1/2)e^a ) (1/2)t^2 −t+1=(1/4)e^a t^2 −(1/2)e^a t+(1/2)e^a (1/2)t^2 −t+1=(1/2)e^a ((1/2)t^2 −t+1) 1=(1/2)e^a e^a =2 e^a =e^(ln 2) a=ln 2
$${h}\left({x}\right)={f}\left({x}−\mathrm{ln}\:\mathrm{2}\right)+{a} \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{x}} −{e}^{{x}} +\mathrm{1}\right)=\mathrm{ln}\:\left({e}^{\mathrm{2}\left({x}−\mathrm{ln}\:\mathrm{2}\right)} −{e}^{{x}−\mathrm{ln}\:\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)+{a} \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{x}} −{e}^{{x}} +\mathrm{1}\right)=\mathrm{ln}\:\left({e}^{\mathrm{2}{x}−\mathrm{ln}\:\mathrm{4}} −{e}^{{x}−\mathrm{ln}\:\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)+{a} \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{x}} −{e}^{{x}} +\mathrm{1}\right)=\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{2}{x}} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}}\right)+{a} \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{x}} −{e}^{{x}} +\mathrm{1}\right)=\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{2}{x}} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{ln}\:{e}^{{a}} \\ $$$$ \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{x}} −{e}^{{x}} +\mathrm{1}\right)=\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{4}}{e}^{{a}} {e}^{\mathrm{2}{x}} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} {e}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} \right) \\ $$$${Let}\:{t}={e}^{{x}} ,\:{therefore} \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} −{t}+\mathrm{1}\right)=\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{4}}{e}^{{a}} {t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} {t}+\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} −{t}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{4}}{e}^{{a}} {t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} {t}+\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} −{t}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} \left(\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} −{t}+\mathrm{1}\right) \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}{e}^{{a}} \\ $$$${e}^{{a}} =\mathrm{2} \\ $$$${e}^{{a}} ={e}^{\mathrm{ln}\:\mathrm{2}} \\ $$$${a}=\mathrm{ln}\:\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *