Question Number 167011 by mnjuly1970 last updated on 04/Mar/22
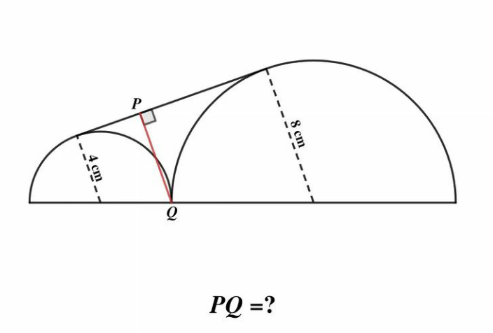
Answered by TheSupreme last updated on 04/Mar/22
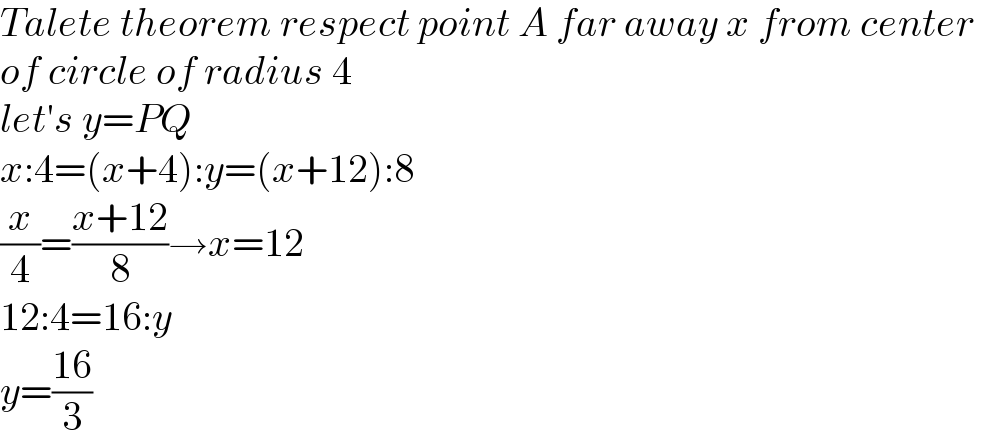
$${Talete}\:{theorem}\:{respect}\:{point}\:{A}\:{far}\:{away}\:{x}\:{from}\:{center}\: \\ $$$${of}\:{circle}\:{of}\:{radius}\:\mathrm{4} \\ $$$${let}'{s}\:{y}={PQ} \\ $$$${x}:\mathrm{4}=\left({x}+\mathrm{4}\right):{y}=\left({x}+\mathrm{12}\right):\mathrm{8} \\ $$$$\frac{{x}}{\mathrm{4}}=\frac{{x}+\mathrm{12}}{\mathrm{8}}\rightarrow{x}=\mathrm{12} \\ $$$$\mathrm{12}:\mathrm{4}=\mathrm{16}:{y} \\ $$$${y}=\frac{\mathrm{16}}{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 19/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Lahsen last updated on 05/Mar/22

$${PQ}=\mathrm{4}+\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{16}}{\mathrm{3}} \\ $$
