Question Number 167013 by amin96 last updated on 04/Mar/22

Answered by mr W last updated on 05/Mar/22

Commented by Tawa11 last updated on 06/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 05/Mar/22
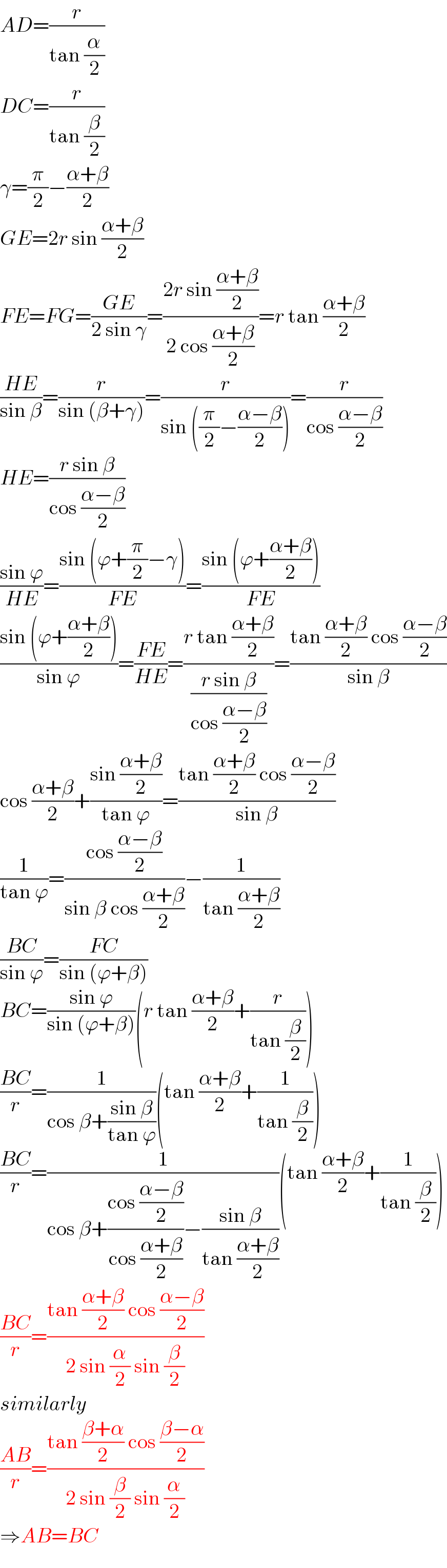
$${AD}=\frac{{r}}{\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}} \\ $$$${DC}=\frac{{r}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}} \\ $$$$\gamma=\frac{\pi}{\mathrm{2}}−\frac{\alpha+\beta}{\mathrm{2}} \\ $$$${GE}=\mathrm{2}{r}\:\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$${FE}={FG}=\frac{{GE}}{\mathrm{2}\:\mathrm{sin}\:\gamma}=\frac{\mathrm{2}{r}\:\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}}{\mathrm{2}\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}}}={r}\:\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\frac{{HE}}{\mathrm{sin}\:\beta}=\frac{{r}}{\mathrm{sin}\:\left(\beta+\gamma\right)}=\frac{{r}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\alpha−\beta}{\mathrm{2}}\right)}=\frac{{r}}{\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}} \\ $$$${HE}=\frac{{r}\:\mathrm{sin}\:\beta}{\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}} \\ $$$$\frac{\mathrm{sin}\:\varphi}{{HE}}=\frac{\mathrm{sin}\:\left(\varphi+\frac{\pi}{\mathrm{2}}−\gamma\right)}{{FE}}=\frac{\mathrm{sin}\:\left(\varphi+\frac{\alpha+\beta}{\mathrm{2}}\right)}{{FE}} \\ $$$$\frac{\mathrm{sin}\:\left(\varphi+\frac{\alpha+\beta}{\mathrm{2}}\right)}{\mathrm{sin}\:\varphi}=\frac{{FE}}{{HE}}=\frac{{r}\:\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}}{\frac{{r}\:\mathrm{sin}\:\beta}{\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}}}=\frac{\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}}{\mathrm{sin}\:\beta} \\ $$$$\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}}+\frac{\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}}{\mathrm{tan}\:\varphi}=\frac{\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}}{\mathrm{sin}\:\beta} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}=\frac{\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}}{\mathrm{sin}\:\beta\:\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}} \\ $$$$\frac{{BC}}{\mathrm{sin}\:\varphi}=\frac{{FC}}{\mathrm{sin}\:\left(\varphi+\beta\right)} \\ $$$${BC}=\frac{\mathrm{sin}\:\varphi}{\mathrm{sin}\:\left(\varphi+\beta\right)}\left({r}\:\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}+\frac{{r}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right) \\ $$$$\frac{{BC}}{{r}}=\frac{\mathrm{1}}{\mathrm{cos}\:\beta+\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\varphi}}\left(\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right) \\ $$$$\frac{{BC}}{{r}}=\frac{\mathrm{1}}{\mathrm{cos}\:\beta+\frac{\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}}{\mathrm{cos}\:\frac{\alpha+\beta}{\mathrm{2}}}−\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}}}\left(\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right) \\ $$$$\frac{{BC}}{{r}}=\frac{\mathrm{tan}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\alpha−\beta}{\mathrm{2}}}{\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}} \\ $$$${similarly} \\ $$$$\frac{{AB}}{{r}}=\frac{\mathrm{tan}\:\frac{\beta+\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta−\alpha}{\mathrm{2}}}{\mathrm{2}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}} \\ $$$$\Rightarrow{AB}={BC} \\ $$
