Question Number 167027 by Tawa11 last updated on 04/Mar/22

Commented by cortano1 last updated on 05/Mar/22
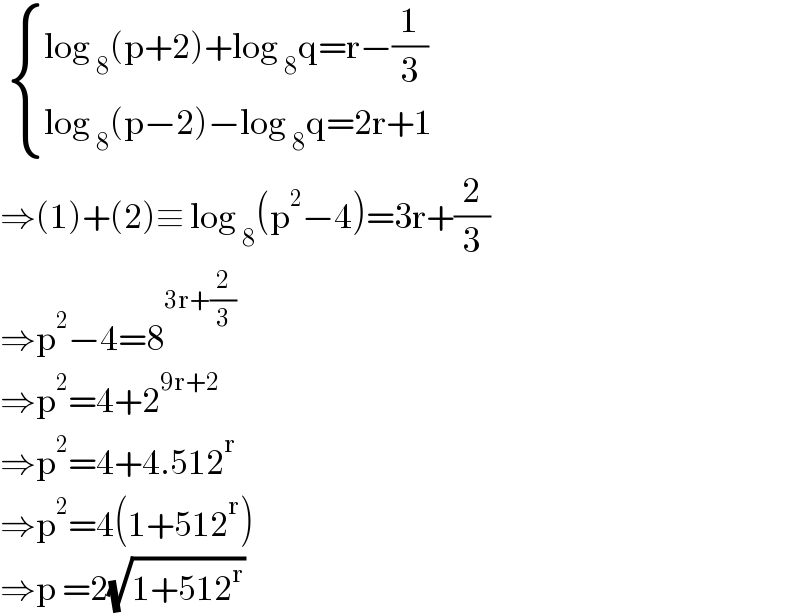
$$\:\begin{cases}{\mathrm{log}\:_{\mathrm{8}} \left(\mathrm{p}+\mathrm{2}\right)+\mathrm{log}\:_{\mathrm{8}} \mathrm{q}=\mathrm{r}−\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{log}\:_{\mathrm{8}} \left(\mathrm{p}−\mathrm{2}\right)−\mathrm{log}\:_{\mathrm{8}} \mathrm{q}=\mathrm{2r}+\mathrm{1}}\end{cases} \\ $$$$\Rightarrow\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\equiv\:\mathrm{log}\:_{\mathrm{8}} \left(\mathrm{p}^{\mathrm{2}} −\mathrm{4}\right)=\mathrm{3r}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{8}^{\mathrm{3r}+\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{p}^{\mathrm{2}} =\mathrm{4}+\mathrm{2}^{\mathrm{9r}+\mathrm{2}} \\ $$$$\Rightarrow\mathrm{p}^{\mathrm{2}} =\mathrm{4}+\mathrm{4}.\mathrm{512}^{\mathrm{r}} \\ $$$$\Rightarrow\mathrm{p}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}+\mathrm{512}^{\mathrm{r}} \right) \\ $$$$\Rightarrow\mathrm{p}\:=\mathrm{2}\sqrt{\mathrm{1}+\mathrm{512}^{\mathrm{r}} } \\ $$
