Question Number 167043 by mnjuly1970 last updated on 05/Mar/22
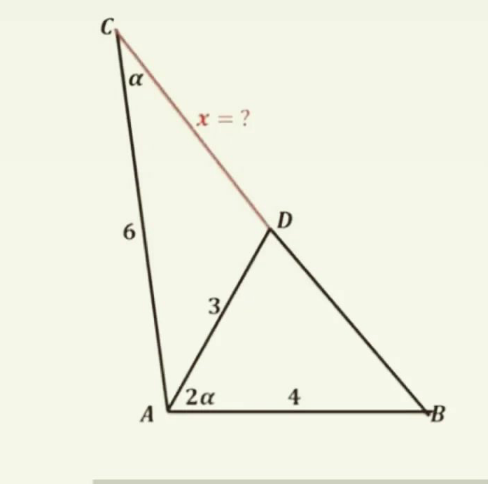
Answered by mr W last updated on 05/Mar/22
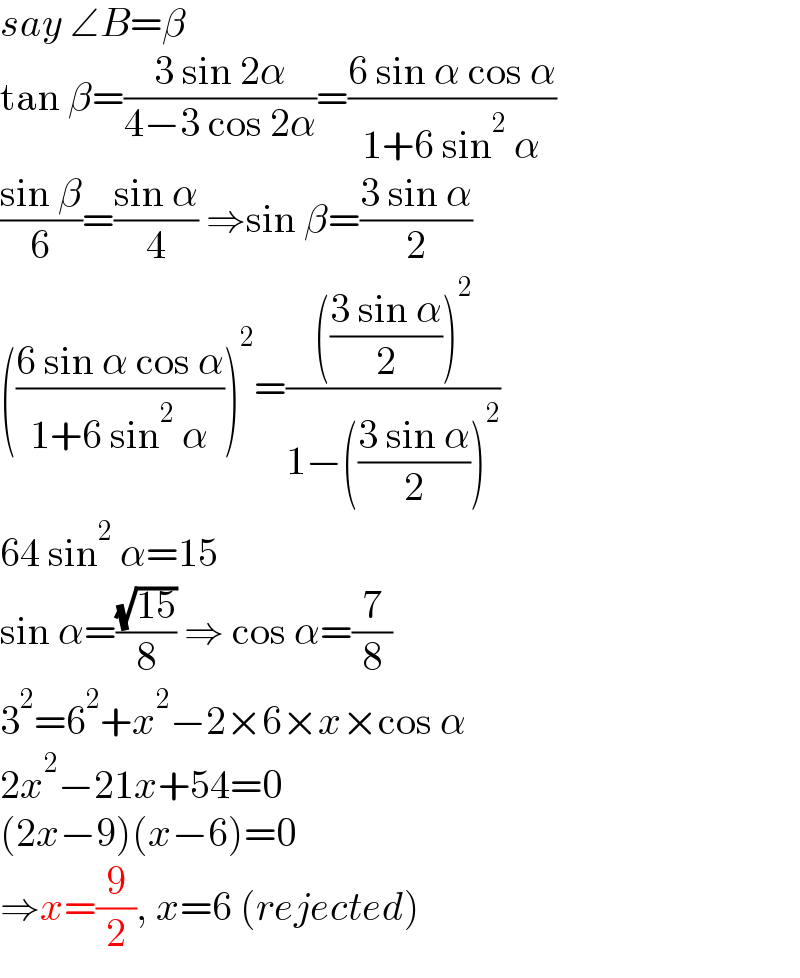
$${say}\:\angle{B}=\beta \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{4}−\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\alpha}=\frac{\mathrm{6}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}{\mathrm{1}+\mathrm{6}\:\mathrm{sin}^{\mathrm{2}} \:\alpha} \\ $$$$\frac{\mathrm{sin}\:\beta}{\mathrm{6}}=\frac{\mathrm{sin}\:\alpha}{\mathrm{4}}\:\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{3}\:\mathrm{sin}\:\alpha}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{6}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha}{\mathrm{1}+\mathrm{6}\:\mathrm{sin}^{\mathrm{2}} \:\alpha}\right)^{\mathrm{2}} =\frac{\left(\frac{\mathrm{3}\:\mathrm{sin}\:\alpha}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{1}−\left(\frac{\mathrm{3}\:\mathrm{sin}\:\alpha}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{64}\:\mathrm{sin}^{\mathrm{2}} \:\alpha=\mathrm{15} \\ $$$$\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{15}}}{\mathrm{8}}\:\Rightarrow\:\mathrm{cos}\:\alpha=\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\mathrm{3}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}×\mathrm{6}×{x}×\mathrm{cos}\:\alpha \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{54}=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}−\mathrm{9}\right)\left({x}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{9}}{\mathrm{2}},\:{x}=\mathrm{6}\:\left({rejected}\right) \\ $$
Commented by mnjuly1970 last updated on 05/Mar/22
$$\:{Sir}\:{W}\::\:{thank}\:{you}\:{so}\:{much} \\ $$$$\:\:\:\:\:\left({grateful}\right)^{\:\infty} \\ $$
Commented by Tawa11 last updated on 05/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
