Question Number 167082 by cortano1 last updated on 06/Mar/22

Commented by cortano1 last updated on 06/Mar/22
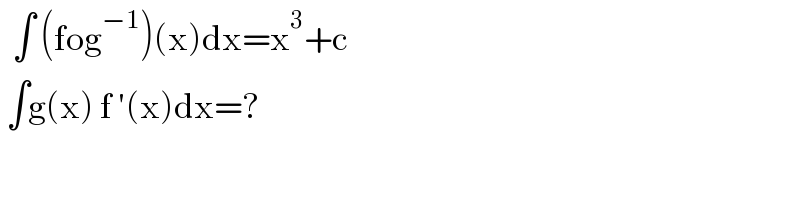
$$\:\:\int\:\left(\mathrm{fog}^{−\mathrm{1}} \right)\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{x}^{\mathrm{3}} +\mathrm{c} \\ $$$$\:\int\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{f}\:'\left(\mathrm{x}\right)\mathrm{dx}=?\: \\ $$
Answered by greogoury55 last updated on 06/Mar/22
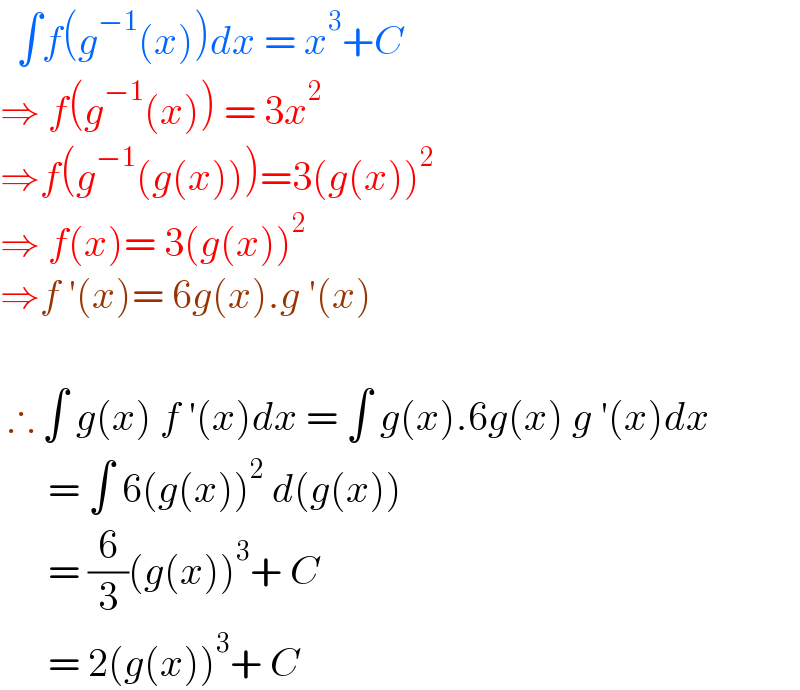
$$\:\:\int{f}\left({g}^{−\mathrm{1}} \left({x}\right)\right){dx}\:=\:{x}^{\mathrm{3}} +{C} \\ $$$$\Rightarrow\:{f}\left({g}^{−\mathrm{1}} \left({x}\right)\right)\:=\:\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({g}^{−\mathrm{1}} \left({g}\left({x}\right)\right)\right)=\mathrm{3}\left({g}\left({x}\right)\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{f}\left({x}\right)=\:\mathrm{3}\left({g}\left({x}\right)\right)^{\mathrm{2}} \\ $$$$\Rightarrow{f}\:'\left({x}\right)=\:\mathrm{6}{g}\left({x}\right).{g}\:'\left({x}\right)\: \\ $$$$ \\ $$$$\:\therefore\:\int\:{g}\left({x}\right)\:{f}\:'\left({x}\right){dx}\:=\:\int\:{g}\left({x}\right).\mathrm{6}{g}\left({x}\right)\:{g}\:'\left({x}\right){dx} \\ $$$$\:\:\:\:\:\:=\:\int\:\mathrm{6}\left({g}\left({x}\right)\right)^{\mathrm{2}} \:{d}\left({g}\left({x}\right)\right) \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{6}}{\mathrm{3}}\left({g}\left({x}\right)\right)^{\mathrm{3}} +\:{C} \\ $$$$\:\:\:\:\:\:=\:\mathrm{2}\left({g}\left({x}\right)\right)^{\mathrm{3}} +\:{C}\: \\ $$
