Question Number 167215 by Avijit007 last updated on 09/Mar/22

Answered by MikeH last updated on 09/Mar/22
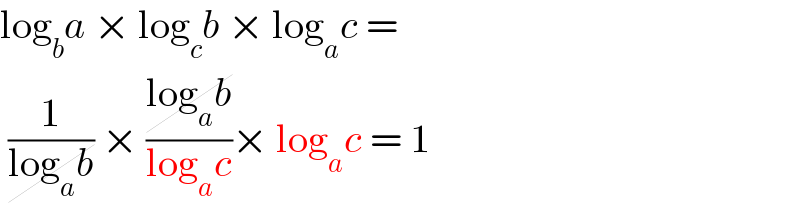
$$\mathrm{log}_{{b}} {a}\:×\:\mathrm{log}_{{c}} {b}\:×\:\mathrm{log}_{{a}} {c}\:= \\ $$$$\:\frac{\mathrm{1}}{\cancel{\mathrm{log}_{{a}} {b}}}\:×\:\frac{\cancel{\mathrm{log}_{{a}} {b}}}{\mathrm{log}_{{a}} {c}}×\:\mathrm{log}_{{a}} {c}\:=\:\mathrm{1} \\ $$
Answered by MikeH last updated on 09/Mar/22
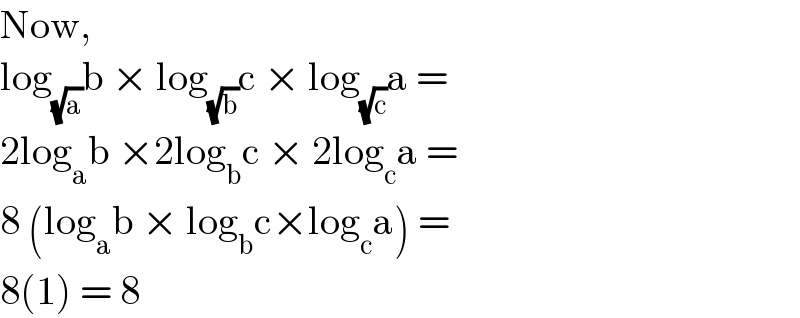
$$\mathrm{Now}, \\ $$$$\mathrm{log}_{\sqrt{\mathrm{a}}} \mathrm{b}\:×\:\mathrm{log}_{\sqrt{\mathrm{b}}} \mathrm{c}\:×\:\mathrm{log}_{\sqrt{\mathrm{c}}} \mathrm{a}\:=\: \\ $$$$\mathrm{2log}_{\mathrm{a}} \mathrm{b}\:×\mathrm{2log}_{\mathrm{b}} \mathrm{c}\:×\:\mathrm{2log}_{\mathrm{c}} \mathrm{a}\:= \\ $$$$\mathrm{8}\:\left(\mathrm{log}_{\mathrm{a}} \mathrm{b}\:×\:\mathrm{log}_{\mathrm{b}} \mathrm{c}×\mathrm{log}_{\mathrm{c}} \mathrm{a}\right)\:= \\ $$$$\mathrm{8}\left(\mathrm{1}\right)\:=\:\mathrm{8} \\ $$
