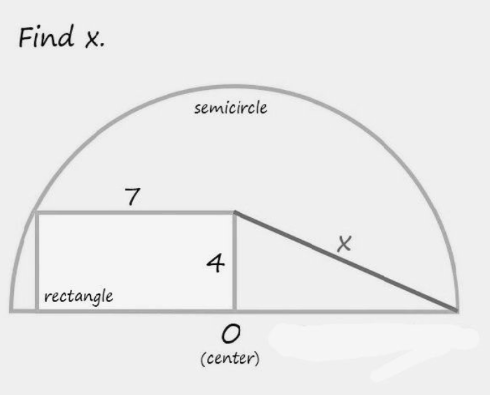
Question Number 167339 by mnjuly1970 last updated on 13/Mar/22
Commented by Tawa11 last updated on 19/Mar/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by greogoury55 last updated on 13/Mar/22
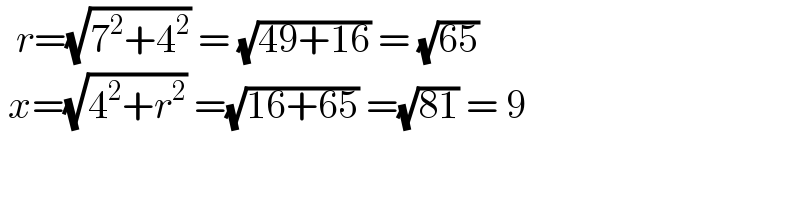
$$\:\:{r}=\sqrt{\mathrm{7}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{49}+\mathrm{16}}\:=\:\sqrt{\mathrm{65}} \\ $$$$\:{x}=\sqrt{\mathrm{4}^{\mathrm{2}} +{r}^{\mathrm{2}} }\:=\sqrt{\mathrm{16}+\mathrm{65}}\:=\sqrt{\mathrm{81}}\:=\:\mathrm{9} \\ $$
Answered by som(math1967) last updated on 13/Mar/22
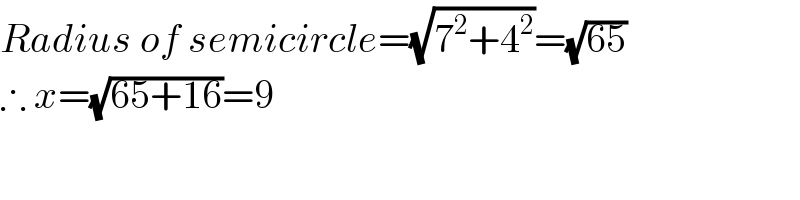
$${Radius}\:{of}\:{semicircle}=\sqrt{\mathrm{7}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }=\sqrt{\mathrm{65}} \\ $$$$\therefore\:{x}=\sqrt{\mathrm{65}+\mathrm{16}}=\mathrm{9} \\ $$
