Question-167374

Question Number 167374 by mathlove last updated on 14/Mar/22

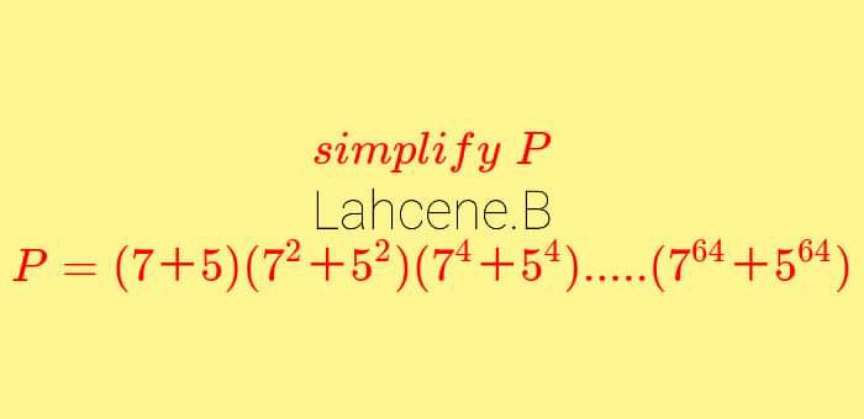
Answered by nurtani last updated on 14/Mar/22

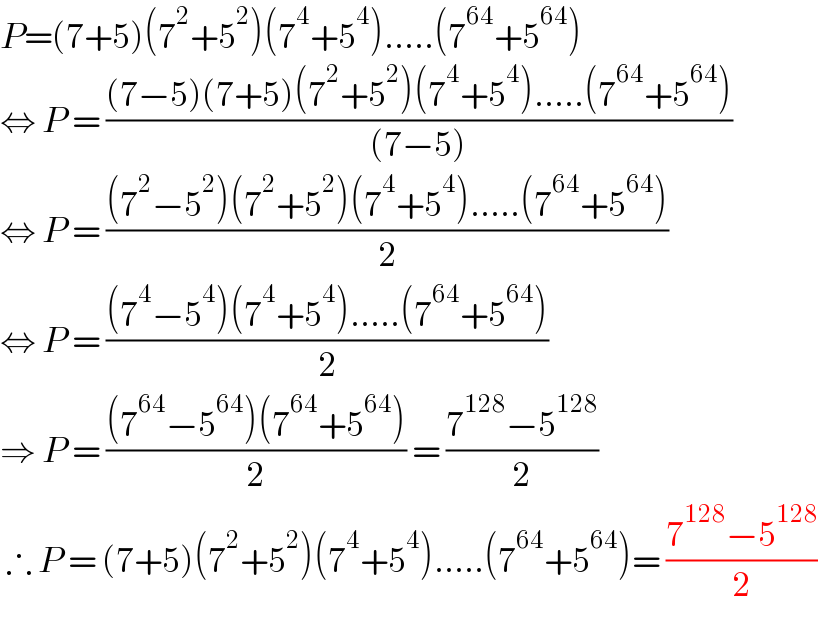
P=(7+5)(7^2 +5^2 )(7^4 +5^4 ).....(7^(64) +5^(64) ) ⇔ P = (((7−5)(7+5)(7^2 +5^2 )(7^4 +5^4 ).....(7^(64) +5^(64) ))/((7−5))) ⇔ P = (((7^2 −5^2 )(7^2 +5^2 )(7^4 +5^4 ).....(7^(64) +5^(64) ))/2) ⇔ P = (((7^4 −5^4 )(7^4 +5^4 ).....(7^(64) +5^(64) ))/2) ⇒ P = (((7^(64) −5^(64) )(7^(64) +5^(64) ))/2) = ((7^(128) −5^(128) )/2) ∴ P = (7+5)(7^2 +5^2 )(7^4 +5^4 ).....(7^(64) +5^(64) )= ((7^(128) −5^(128) )/2)

$${P}=\left(\mathrm{7}+\mathrm{5}\right)\left(\mathrm{7}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right)\left(\mathrm{7}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} \right)…..\left(\mathrm{7}^{\mathrm{64}} +\mathrm{5}^{\mathrm{64}} \right) \\ $$$$\Leftrightarrow\:{P}\:=\:\frac{\left(\mathrm{7}−\mathrm{5}\right)\left(\mathrm{7}+\mathrm{5}\right)\left(\mathrm{7}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right)\left(\mathrm{7}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} \right)…..\left(\mathrm{7}^{\mathrm{64}} +\mathrm{5}^{\mathrm{64}} \right)}{\left(\mathrm{7}−\mathrm{5}\right)} \\ $$$$\Leftrightarrow\:{P}\:=\:\frac{\left(\mathrm{7}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} \right)\left(\mathrm{7}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right)\left(\mathrm{7}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} \right)…..\left(\mathrm{7}^{\mathrm{64}} +\mathrm{5}^{\mathrm{64}} \right)}{\mathrm{2}} \\ $$$$\Leftrightarrow\:{P}\:=\:\frac{\left(\mathrm{7}^{\mathrm{4}} −\mathrm{5}^{\mathrm{4}} \right)\left(\mathrm{7}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} \right)…..\left(\mathrm{7}^{\mathrm{64}} +\mathrm{5}^{\mathrm{64}} \right)}{\mathrm{2}} \\ $$$$\Rightarrow\:{P}\:=\:\frac{\left(\mathrm{7}^{\mathrm{64}} −\mathrm{5}^{\mathrm{64}} \right)\left(\mathrm{7}^{\mathrm{64}} +\mathrm{5}^{\mathrm{64}} \right)}{\mathrm{2}}\:=\:\frac{\mathrm{7}^{\mathrm{128}} −\mathrm{5}^{\mathrm{128}} }{\mathrm{2}} \\ $$$$\:\therefore\:{P}\:=\:\left(\mathrm{7}+\mathrm{5}\right)\left(\mathrm{7}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right)\left(\mathrm{7}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} \right)…..\left(\mathrm{7}^{\mathrm{64}} +\mathrm{5}^{\mathrm{64}} \right)=\:\frac{\mathrm{7}^{\mathrm{128}} −\mathrm{5}^{\mathrm{128}} }{\mathrm{2}} \\ $$

Commented by TheSupreme last updated on 15/Mar/22

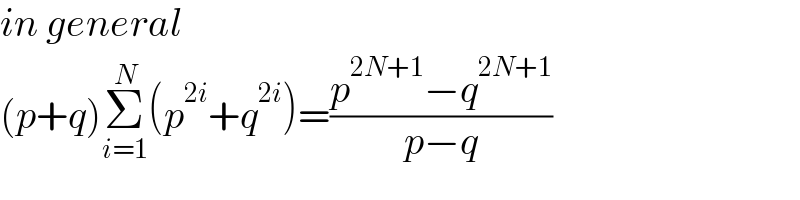
in general (p+q)Σ_(i=1) ^N (p^(2i) +q^(2i) )=((p^(2N+1) −q^(2N+1) )/(p−q))

$${in}\:{general} \\ $$$$\left({p}+{q}\right)\underset{{i}=\mathrm{1}} {\overset{{N}} {\sum}}\left({p}^{\mathrm{2}{i}} +{q}^{\mathrm{2}{i}} \right)=\frac{{p}^{\mathrm{2}{N}+\mathrm{1}} −{q}^{\mathrm{2}{N}+\mathrm{1}} }{{p}−{q}} \\ $$

Answered by som(math1967) last updated on 14/Mar/22

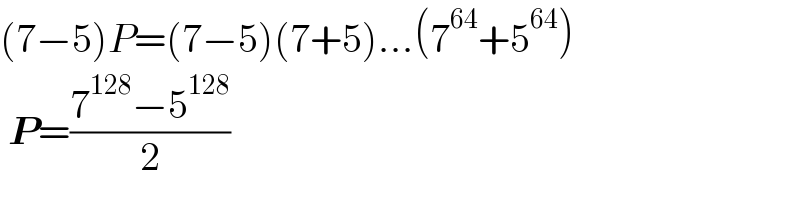
(7−5)P=(7−5)(7+5)...(7^(64) +5^(64) ) P=((7^(128) −5^(128) )/2)

$$\left(\mathrm{7}−\mathrm{5}\right){P}=\left(\mathrm{7}−\mathrm{5}\right)\left(\mathrm{7}+\mathrm{5}\right)…\left(\mathrm{7}^{\mathrm{64}} +\mathrm{5}^{\mathrm{64}} \right) \\ $$$$\:\boldsymbol{{P}}=\frac{\mathrm{7}^{\mathrm{128}} −\mathrm{5}^{\mathrm{128}} }{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply