Menu Close

Question-167400

Tinku Tara 0 Comments
Pin




Question Number 167400 by infinityaction last updated on 15/Mar/22
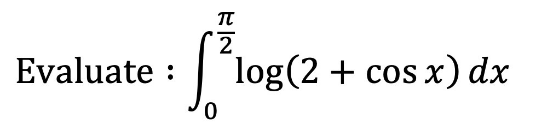
Answered by Mathspace last updated on 16/Mar/22
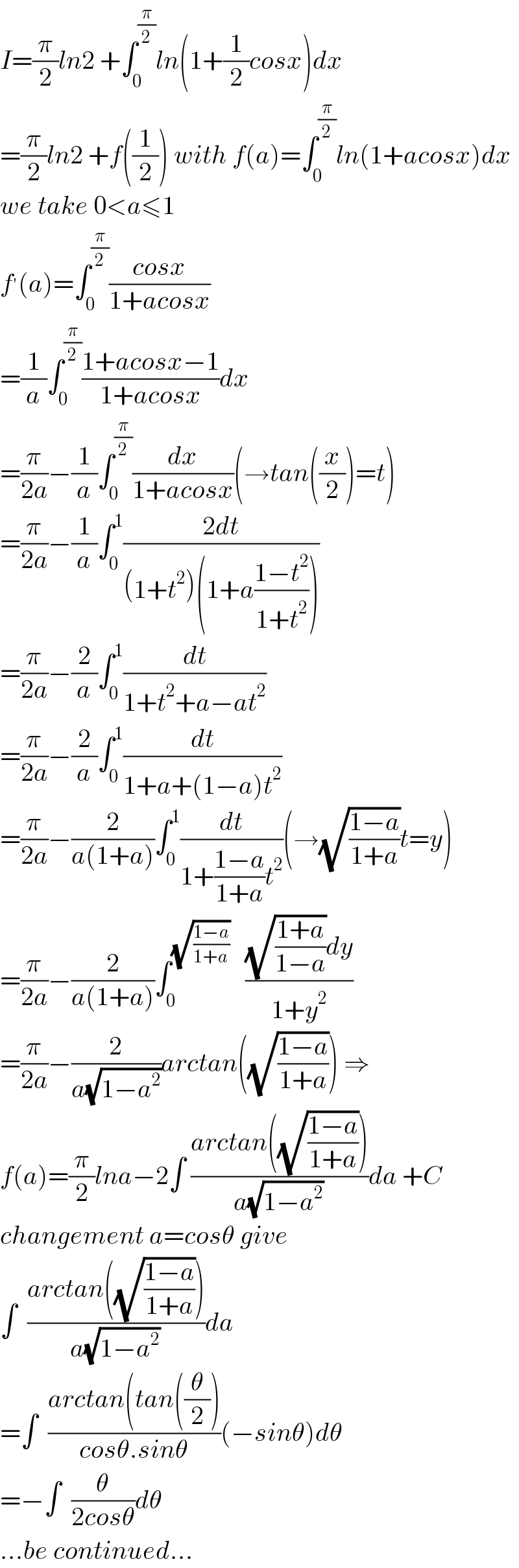
I=(π/2)ln2 +∫_0 ^(π/2) ln(1+(1/2)cosx)dx =(π/2)ln2 +f((1/2)) with f(a)=∫_0 ^(π/2) ln(1+acosx)dx we take 0<a≤1 f^′ (a)=∫_0 ^(π/2) ((cosx)/(1+acosx)) =(1/a)∫_0 ^(π/2) ((1+acosx−1)/(1+acosx))dx =(π/(2a))−(1/a)∫_0 ^(π/2) (dx/(1+acosx))(→tan((x/2))=t) =(π/(2a))−(1/a)∫_0 ^1 ((2dt)/((1+t^2 )(1+a((1−t^2 )/(1+t^2 ))))) =(π/(2a))−(2/a)∫_0 ^1 (dt/(1+t^2 +a−at^2 )) =(π/(2a))−(2/a)∫_0 ^1 (dt/(1+a+(1−a)t^2 )) =(π/(2a))−(2/(a(1+a)))∫_0 ^1 (dt/(1+((1−a)/(1+a))t^2 ))(→(√((1−a)/(1+a)))t=y) =(π/(2a))−(2/(a(1+a)))∫_0 ^(√((1−a)/(1+a))) (((√((1+a)/(1−a)))dy)/(1+y^2 )) =(π/(2a))−(2/(a(√(1−a^2 ))))arctan((√((1−a)/(1+a)))) ⇒ f(a)=(π/2)lna−2∫ ((arctan((√((1−a)/(1+a)))))/(a(√(1−a^2 ))))da +C changement a=cosθ give ∫ ((arctan((√((1−a)/(1+a)))))/(a(√(1−a^2 ))))da =∫ ((arctan(tan((θ/2)))/(cosθ.sinθ))(−sinθ)dθ =−∫ (θ/(2cosθ))dθ ...be continued...
$${I}=\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{cosx}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}\:+{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:{with}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{acosx}\right){dx} \\ $$$${we}\:{take}\:\mathrm{0}<{a}\leqslant\mathrm{1} \\ $$$${f}^{'} \left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{\mathrm{1}+{acosx}} \\ $$$$=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+{acosx}−\mathrm{1}}{\mathrm{1}+{acosx}}{dx} \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+{acosx}}\left(\rightarrow{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\right) \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{2}}{{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +{a}−{at}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{2}}{{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{a}+\left(\mathrm{1}−{a}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{2}}{{a}\left(\mathrm{1}+{a}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}{t}^{\mathrm{2}} }\left(\rightarrow\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}{t}={y}\right) \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{2}}{{a}\left(\mathrm{1}+{a}\right)}\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}} \:\:\:\frac{\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}{dy}}{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{2}}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}\right)\:\Rightarrow \\ $$$${f}\left({a}\right)=\frac{\pi}{\mathrm{2}}{lna}−\mathrm{2}\int\:\frac{{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}\right)}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{da}\:+{C} \\ $$$${changement}\:{a}={cos}\theta\:{give} \\ $$$$\int\:\:\frac{{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}\right)}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{da} \\ $$$$=\int\:\:\frac{{arctan}\left({tan}\left(\frac{\theta}{\mathrm{2}}\right)\right.}{{cos}\theta.{sin}\theta}\left(−{sin}\theta\right){d}\theta \\ $$$$=−\int\:\:\frac{\theta}{\mathrm{2}{cos}\theta}{d}\theta \\ $$$$…{be}\:{continued}… \\ $$
Commented by infinityaction last updated on 16/Mar/22
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by mindispower last updated on 16/Mar/22
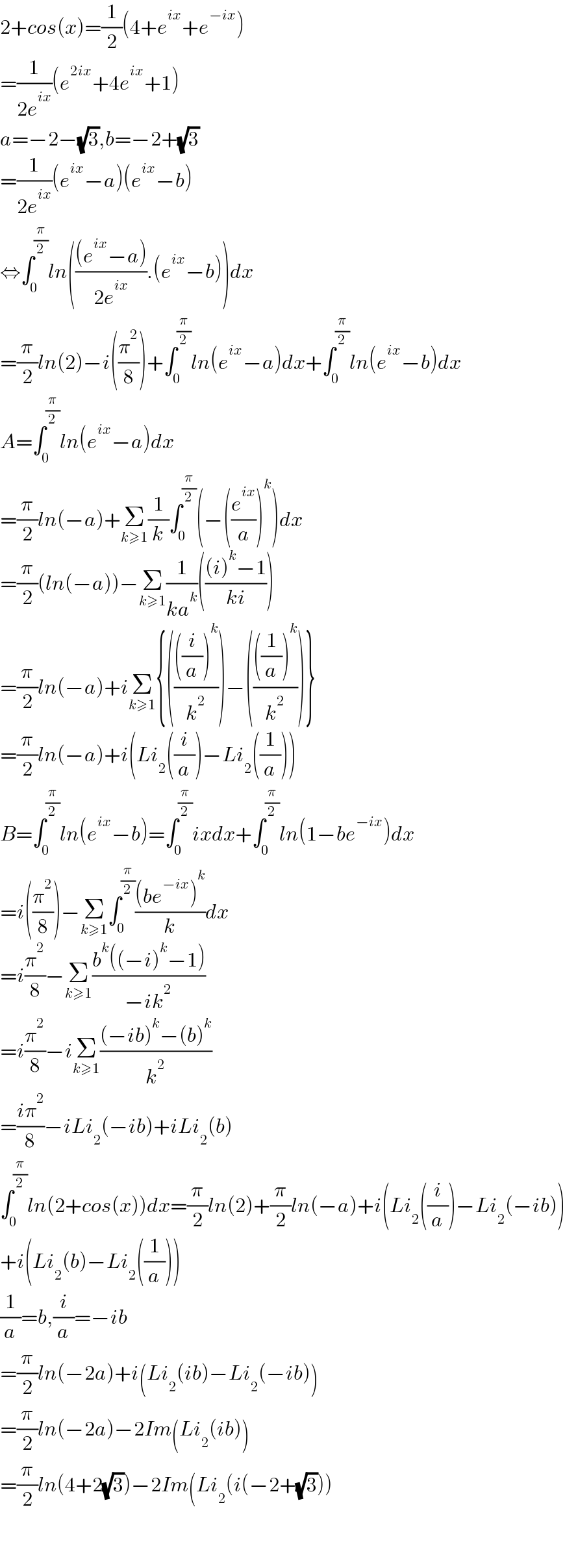
2+cos(x)=(1/2)(4+e^(ix) +e^(−ix) ) =(1/(2e^(ix) ))(e^(2ix) +4e^(ix) +1) a=−2−(√3),b=−2+(√3) =(1/(2e^(ix) ))(e^(ix) −a)(e^(ix) −b) ⇔∫_0 ^(π/2) ln((((e^(ix) −a))/(2e^(ix) )).(e^(ix) −b))dx =(π/2)ln(2)−i((π^2 /8))+∫_0 ^(π/2) ln(e^(ix) −a)dx+∫_0 ^(π/2) ln(e^(ix) −b)dx A=∫_0 ^(π/2) ln(e^(ix) −a)dx =(π/2)ln(−a)+Σ_(k≥1) (1/k)∫_0 ^(π/2) (−((e^(ix) /a))^k )dx =(π/2)(ln(−a))−Σ_(k≥1) (1/(ka^k ))((((i)^k −1)/(ki))) =(π/2)ln(−a)+iΣ_(k≥1) {(((((i/a))^k )/k^2 ))−(((((1/a))^k )/k^2 ))} =(π/2)ln(−a)+i(Li_2 ((i/a))−Li_2 ((1/a))) B=∫_0 ^(π/2) ln(e^(ix) −b)=∫_0 ^(π/2) ixdx+∫_0 ^(π/2) ln(1−be^(−ix) )dx =i((π^2 /8))−Σ_(k≥1) ∫_0 ^(π/2) (((be^(−ix) )^k )/k)dx =i(π^2 /8)−Σ_(k≥1) ((b^k ((−i)^k −1))/(−ik^2 )) =i(π^2 /8)−iΣ_(k≥1) (((−ib)^k −(b)^k )/k^2 ) =((iπ^2 )/8)−iLi_2 (−ib)+iLi_2 (b) ∫_0 ^(π/2) ln(2+cos(x))dx=(π/2)ln(2)+(π/2)ln(−a)+i(Li_2 ((i/a))−Li_2 (−ib)) +i(Li_2 (b)−Li_2 ((1/a))) (1/a)=b,(i/a)=−ib =(π/2)ln(−2a)+i(Li_2 (ib)−Li_2 (−ib)) =(π/2)ln(−2a)−2Im(Li_2 (ib)) =(π/2)ln(4+2(√3))−2Im(Li_2 (i(−2+(√3)))
$$\mathrm{2}+{cos}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}+{e}^{{ix}} +{e}^{−{ix}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{e}^{{ix}} }\left({e}^{\mathrm{2}{ix}} +\mathrm{4}{e}^{{ix}} +\mathrm{1}\right) \\ $$$${a}=−\mathrm{2}−\sqrt{\mathrm{3}},{b}=−\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{e}^{{ix}} }\left({e}^{{ix}} −{a}\right)\left({e}^{{ix}} −{b}\right) \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\frac{\left({e}^{{ix}} −{a}\right)}{\mathrm{2}{e}^{{ix}} }.\left({e}^{{ix}} −{b}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−{i}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({e}^{{ix}} −{a}\right){dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({e}^{{ix}} −{b}\right){dx} \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({e}^{{ix}} −{a}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(−{a}\right)+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{k}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(−\left(\frac{{e}^{{ix}} }{{a}}\right)^{{k}} \right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\left({ln}\left(−{a}\right)\right)−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{ka}^{{k}} }\left(\frac{\left({i}\right)^{{k}} −\mathrm{1}}{{ki}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(−{a}\right)+{i}\underset{{k}\geqslant\mathrm{1}} {\sum}\left\{\left(\frac{\left(\frac{{i}}{{a}}\right)^{{k}} }{{k}^{\mathrm{2}} }\right)−\left(\frac{\left(\frac{\mathrm{1}}{{a}}\right)^{{k}} }{{k}^{\mathrm{2}} }\right)\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(−{a}\right)+{i}\left({Li}_{\mathrm{2}} \left(\frac{{i}}{{a}}\right)−{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}}\right)\right) \\ $$$${B}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({e}^{{ix}} −{b}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ixdx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}−{be}^{−{ix}} \right){dx} \\ $$$$={i}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\right)−\underset{{k}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({be}^{−{ix}} \right)^{{k}} }{{k}}{dx} \\ $$$$={i}\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{b}^{{k}} \left(\left(−{i}\right)^{{k}} −\mathrm{1}\right)}{−{ik}^{\mathrm{2}} } \\ $$$$={i}\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−{i}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−{ib}\right)^{{k}} −\left({b}\right)^{{k}} }{{k}^{\mathrm{2}} } \\ $$$$=\frac{{i}\pi^{\mathrm{2}} }{\mathrm{8}}−{iLi}_{\mathrm{2}} \left(−{ib}\right)+{iLi}_{\mathrm{2}} \left({b}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}+{cos}\left({x}\right)\right){dx}=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{2}}{ln}\left(−{a}\right)+{i}\left({Li}_{\mathrm{2}} \left(\frac{{i}}{{a}}\right)−{Li}_{\mathrm{2}} \left(−{ib}\right)\right) \\ $$$$+{i}\left({Li}_{\mathrm{2}} \left({b}\right)−{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}}\right)\right) \\ $$$$\frac{\mathrm{1}}{{a}}={b},\frac{{i}}{{a}}=−{ib} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(−\mathrm{2}{a}\right)+{i}\left({Li}_{\mathrm{2}} \left({ib}\right)−{Li}_{\mathrm{2}} \left(−{ib}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(−\mathrm{2}{a}\right)−\mathrm{2}{Im}\left({Li}_{\mathrm{2}} \left({ib}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)−\mathrm{2}{Im}\left({Li}_{\mathrm{2}} \left({i}\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)\right)\right. \\ $$$$ \\ $$$$ \\ $$
Commented by infinityaction last updated on 17/Mar/22
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *