Menu Close

Question-167443

Tinku Tara 0 Comments
Pin




Question Number 167443 by infinityaction last updated on 16/Mar/22
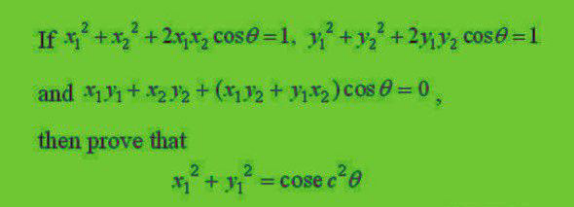
Answered by nimnim last updated on 16/Mar/22
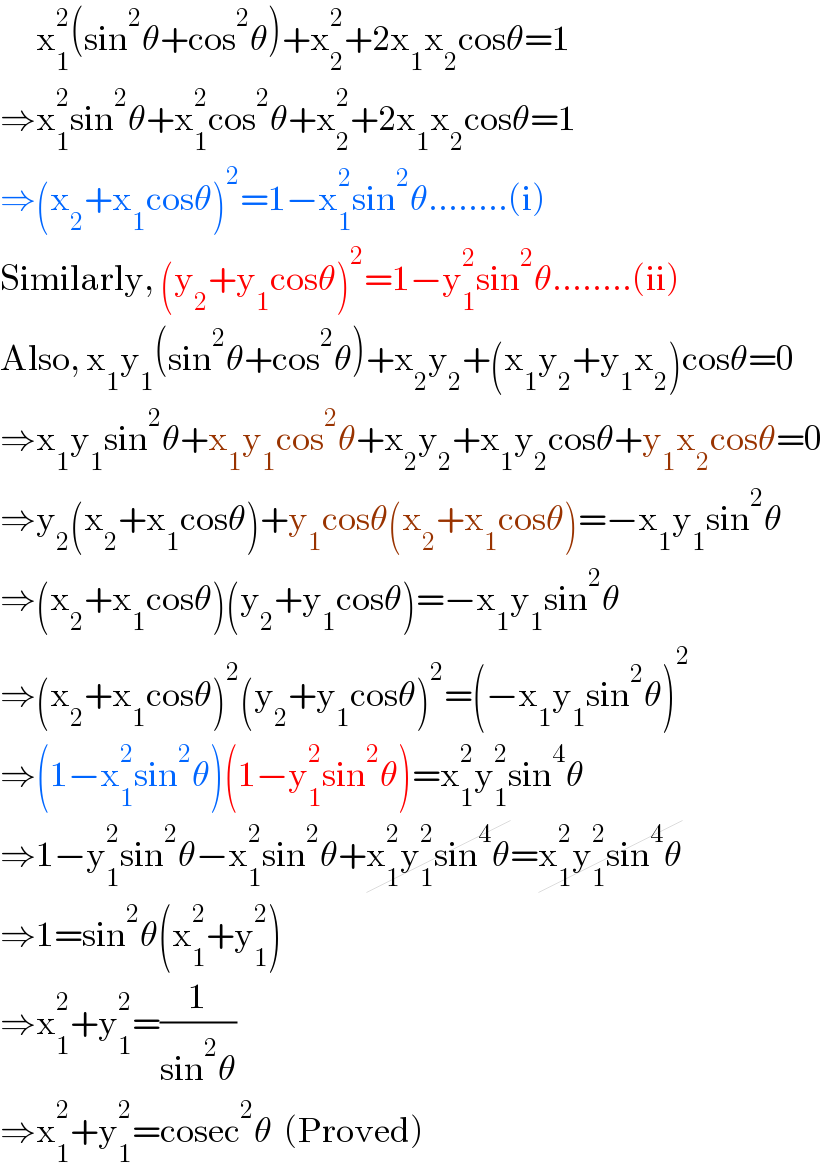
x_1 ^2 (sin^2 θ+cos^2 θ)+x_2 ^2 +2x_1 x_2 cosθ=1 ⇒x_1 ^2 sin^2 θ+x_1 ^2 cos^2 θ+x_2 ^2 +2x_1 x_2 cosθ=1 ⇒(x_2 +x_1 cosθ)^2 =1−x_1 ^2 sin^2 θ........(i) Similarly, (y_2 +y_1 cosθ)^2 =1−y_1 ^2 sin^2 θ........(ii) Also, x_1 y_1 (sin^2 θ+cos^2 θ)+x_2 y_2 +(x_1 y_2 +y_1 x_2 )cosθ=0 ⇒x_1 y_1 sin^2 θ+x_1 y_1 cos^2 θ+x_2 y_2 +x_1 y_2 cosθ+y_1 x_2 cosθ=0 ⇒y_2 (x_2 +x_1 cosθ)+y_1 cosθ(x_2 +x_1 cosθ)=−x_1 y_1 sin^2 θ ⇒(x_2 +x_1 cosθ)(y_2 +y_1 cosθ)=−x_1 y_1 sin^2 θ ⇒(x_2 +x_1 cosθ)^2 (y_2 +y_1 cosθ)^2 =(−x_1 y_1 sin^2 θ)^2 ⇒(1−x_1 ^2 sin^2 θ)(1−y_1 ^2 sin^2 θ)=x_1 ^2 y_1 ^2 sin^4 θ ⇒1−y_1 ^2 sin^2 θ−x_1 ^2 sin^2 θ+x_1 ^2 y_1 ^2 sin^4 θ=x_1 ^2 y_1 ^2 sin^4 θ ⇒1=sin^2 θ(x_1 ^2 +y_1 ^2 ) ⇒x_1 ^2 +y_1 ^2 =(1/(sin^2 θ)) ⇒x_1 ^2 +y_1 ^2 =cosec^2 θ (Proved)
$$\:\:\:\:\:\:\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta\right)+\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} \mathrm{cos}\theta=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta+\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta+\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} \mathrm{cos}\theta=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} \mathrm{cos}\theta\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta……..\left(\mathrm{i}\right) \\ $$$$\mathrm{Similarly},\:\left(\mathrm{y}_{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} \mathrm{cos}\theta\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta……..\left(\mathrm{ii}\right) \\ $$$$\mathrm{Also},\:\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta\right)+\mathrm{x}_{\mathrm{2}} \mathrm{y}_{\mathrm{2}} +\left(\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} \right)\mathrm{cos}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \mathrm{sin}^{\mathrm{2}} \theta+\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \mathrm{cos}^{\mathrm{2}} \theta+\mathrm{x}_{\mathrm{2}} \mathrm{y}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{2}} \mathrm{cos}\theta+\mathrm{y}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} \mathrm{cos}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{2}} \left(\mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} \mathrm{cos}\theta\right)+\mathrm{y}_{\mathrm{1}} \mathrm{cos}\theta\left(\mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} \mathrm{cos}\theta\right)=−\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \mathrm{sin}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\left(\mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} \mathrm{cos}\theta\right)\left(\mathrm{y}_{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} \mathrm{cos}\theta\right)=−\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \mathrm{sin}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\left(\mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{1}} \mathrm{cos}\theta\right)^{\mathrm{2}} \left(\mathrm{y}_{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} \mathrm{cos}\theta\right)^{\mathrm{2}} =\left(−\mathrm{x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \mathrm{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}−\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\right)=\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{4}} \theta \\ $$$$\Rightarrow\mathrm{1}−\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta+\cancel{\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{4}} \theta}=\cancel{\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{4}} \theta} \\ $$$$\Rightarrow\mathrm{1}=\mathrm{sin}^{\mathrm{2}} \theta\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{cosec}^{\mathrm{2}} \theta\:\:\left(\mathrm{Proved}\right) \\ $$
Commented by infinityaction last updated on 17/Mar/22
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *