Question-167550

Question Number 167550 by mathlove last updated on 19/Mar/22

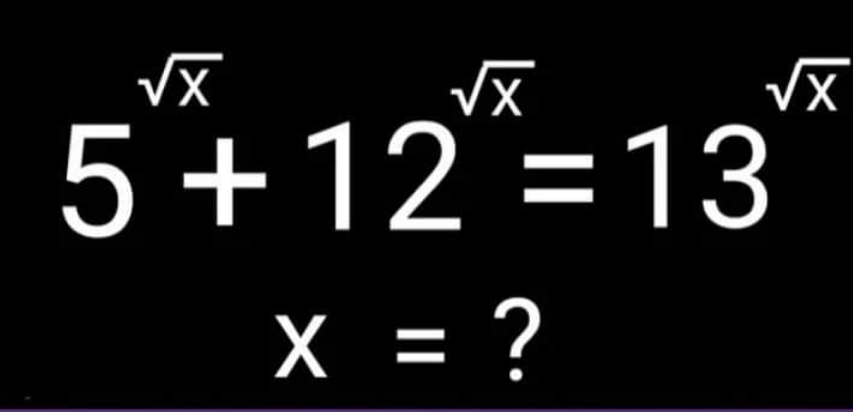
Answered by MJS_new last updated on 19/Mar/22

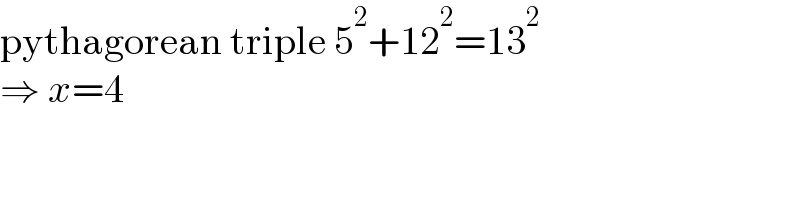
pythagorean triple 5^2 +12^2 =13^2 ⇒ x=4

$$\mathrm{pythagorean}\:\mathrm{triple}\:\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} =\mathrm{13}^{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=\mathrm{4} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Mar/22

5^((√x) ) +12^((√x) ) =13^((√x) ) ((5/(13)))^(√x) +(((12)/(13)))^(√x) =1 Let determinant ((((5/(13))=sin θ))) sin^2 θ=((25)/(169)) ⇒1−cos^2 θ=((25)/(169)) ⇒cos^2 θ=1−((25)/(169)) =((144)/(169))⇒ determinant (((((12)/(13))=cos θ))) (sin θ)^(√x) +(cos θ)^(√x) =1 (sin θ)^(√x) +(cos θ)^(√x) =sin^2 θ+cos^2 θ Comparing exponents on both sides (√x) =2 x=4

$$\mathrm{5}^{\sqrt{{x}}\:} +\mathrm{12}^{\sqrt{{x}}\:} =\mathrm{13}^{\sqrt{{x}}\:} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{13}}\right)^{\sqrt{{x}}} +\left(\frac{\mathrm{12}}{\mathrm{13}}\right)^{\sqrt{{x}}} =\mathrm{1} \\ $$$${Let}\:\begin{array}{|c|}{\frac{\mathrm{5}}{\mathrm{13}}=\mathrm{sin}\:\theta}\\\hline\end{array}\: \\ $$$$\mathrm{sin}^{\mathrm{2}} \theta=\frac{\mathrm{25}}{\mathrm{169}}\:\Rightarrow\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta=\frac{\mathrm{25}}{\mathrm{169}}\: \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \theta=\mathrm{1}−\frac{\mathrm{25}}{\mathrm{169}}\:=\frac{\mathrm{144}}{\mathrm{169}}\Rightarrow\begin{array}{|c|}{\frac{\mathrm{12}}{\mathrm{13}}=\mathrm{cos}\:\theta}\\\hline\end{array} \\ $$$$\left(\mathrm{sin}\:\theta\right)^{\sqrt{{x}}} +\left(\mathrm{cos}\:\theta\right)^{\sqrt{{x}}} =\mathrm{1} \\ $$$$\left(\mathrm{sin}\:\theta\right)^{\sqrt{{x}}} +\left(\mathrm{cos}\:\theta\right)^{\sqrt{{x}}} =\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta \\ $$$${Comparing}\:{exponents}\:{on}\:{both}\:{sides} \\ $$$$\sqrt{{x}}\:=\mathrm{2} \\ $$$${x}=\mathrm{4}\:\: \\ $$

Facebook Tweet Pin

Question-167550

Leave a Reply Cancel reply