Question Number 167566 by infinityaction last updated on 19/Mar/22
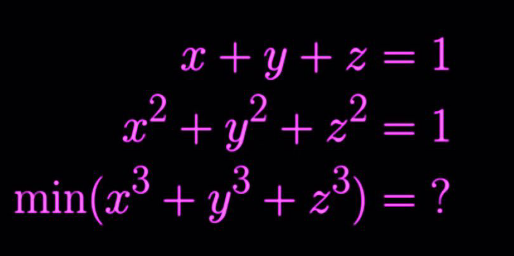
Answered by MJS_new last updated on 19/Mar/22
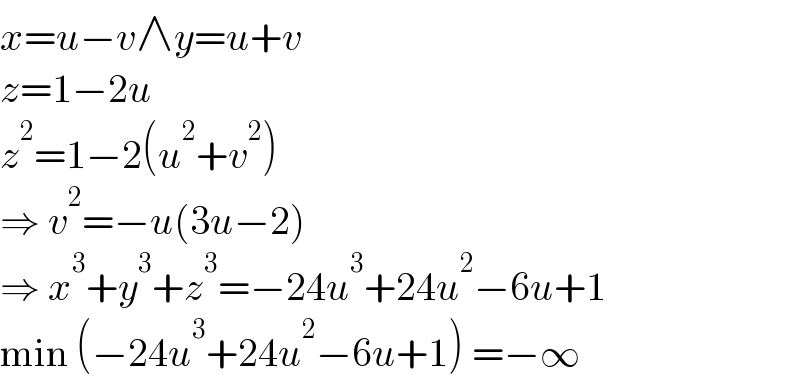
$${x}={u}−{v}\wedge{y}={u}+{v} \\ $$$${z}=\mathrm{1}−\mathrm{2}{u} \\ $$$${z}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{v}^{\mathrm{2}} =−{u}\left(\mathrm{3}{u}−\mathrm{2}\right) \\ $$$$\Rightarrow\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =−\mathrm{24}{u}^{\mathrm{3}} +\mathrm{24}{u}^{\mathrm{2}} −\mathrm{6}{u}+\mathrm{1} \\ $$$$\mathrm{min}\:\left(−\mathrm{24}{u}^{\mathrm{3}} +\mathrm{24}{u}^{\mathrm{2}} −\mathrm{6}{u}+\mathrm{1}\right)\:=−\infty \\ $$
Commented by infinityaction last updated on 19/Mar/22

$${no} \\ $$$${answer}\:{is}\:\mathrm{5}/\mathrm{9} \\ $$
Commented by MJS_new last updated on 19/Mar/22
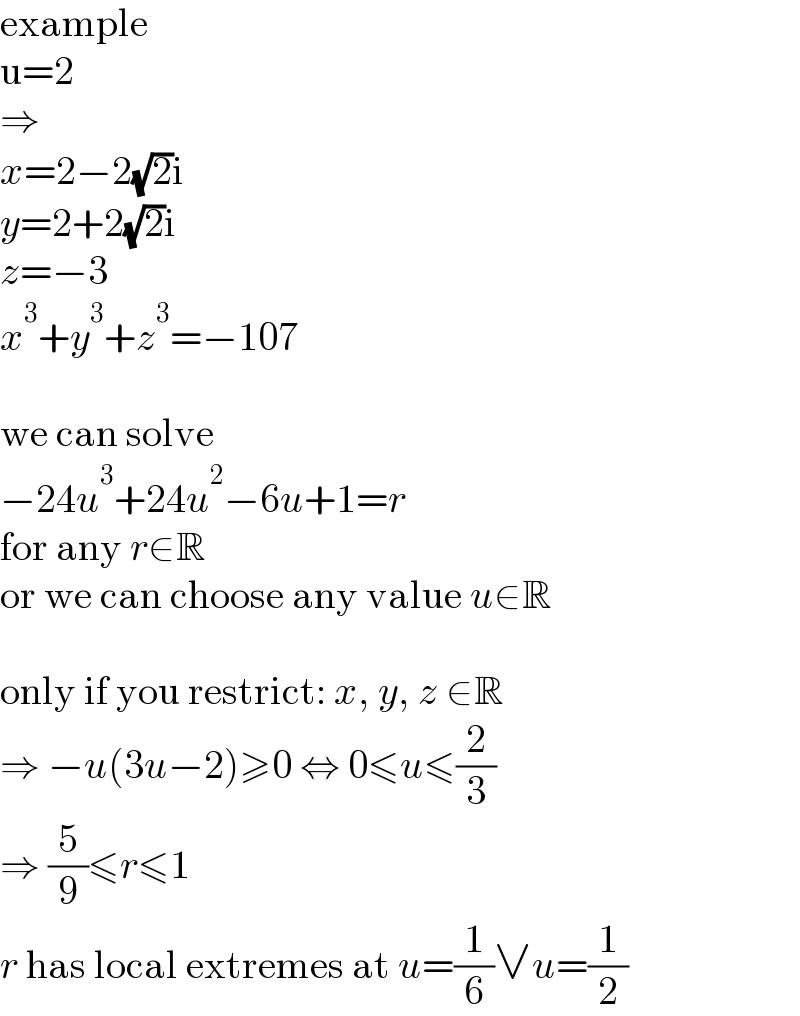
$$\mathrm{example} \\ $$$$\mathrm{u}=\mathrm{2} \\ $$$$\Rightarrow \\ $$$${x}=\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{i} \\ $$$${y}=\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{i} \\ $$$${z}=−\mathrm{3} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =−\mathrm{107} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{solve} \\ $$$$−\mathrm{24}{u}^{\mathrm{3}} +\mathrm{24}{u}^{\mathrm{2}} −\mathrm{6}{u}+\mathrm{1}={r} \\ $$$$\mathrm{for}\:\mathrm{any}\:{r}\in\mathbb{R} \\ $$$$\mathrm{or}\:\mathrm{we}\:\mathrm{can}\:\mathrm{choose}\:\mathrm{any}\:\mathrm{value}\:{u}\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{only}\:\mathrm{if}\:\mathrm{you}\:\mathrm{restrict}:\:{x},\:{y},\:{z}\:\in\mathbb{R} \\ $$$$\Rightarrow\:−{u}\left(\mathrm{3}{u}−\mathrm{2}\right)\geqslant\mathrm{0}\:\Leftrightarrow\:\mathrm{0}\leqslant{u}\leqslant\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\:\frac{\mathrm{5}}{\mathrm{9}}\leqslant{r}\leqslant\mathrm{1} \\ $$$${r}\:\mathrm{has}\:\mathrm{local}\:\mathrm{extremes}\:\mathrm{at}\:{u}=\frac{\mathrm{1}}{\mathrm{6}}\vee{u}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
