Question Number 167593 by cortano1 last updated on 20/Mar/22
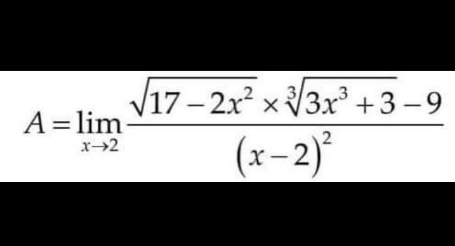
Answered by qaz last updated on 20/Mar/22
![A=lim_(x→0) (((√(17−2(x+2)^2 ))∙((3(x+2)^3 +3))^(1/3) −9)/x^2 ) =lim_(x→0) (((√(9−2x^2 −8x))∙((3x^3 +18x^2 +36x+27))^(1/3) −9)/x^2 ) =9lim_(x→0) (((√(1−(8/9)x−(2/9)x^2 ))∙((1+((36)/(27))x+((18)/(27))x^2 +(3/(27))x^3 ))^(1/3) −1)/x^2 ) =9lim_(x→0) ((ln((√(1−(8/9)x−(2/9)x^2 ))∙((1+((36)/(27))x+((18)/(27))x^2 +(3/(27))x^3 ))^(1/3) ))/x^2 ) =9lim_(x→0) (((1/2)ln(1−(8/9)x−(2/9)x^2 )+(1/3)ln(1+((36)/(27))x+((18)/(27))x^2 +(3/(27))x^3 ))/x^2 ) =9lim_(x→0) (1/(2x))[((−(8/9)−(4/9)x)/(2(1−(8/9)x−(2/9)x^2 )))+((((36)/(27))+((36)/(27))x+(9/(27))x^2 )/(3(1+((36)/(27))x+((28)/(27))x^2 +(3/(27))x^3 )))] =9lim_(x→0) (1/(2x))∙(((−4−2x)/(9−8x−2x^2 ))+((12+12x+3x^2 )/(27+36x+28x^2 +3x^3 ))) =9lim_(x→0) (((−4−2x)(27+36x+28x^2 +3x^3 )+(12+12x+3x^2 )(9−8x−2x^2 ))/(2x(9−8x−2x^2 )(27+36x+28x^2 +3x^3 ))) =9lim_(x→0) (((−4∙36−2∙27+12∙9−12∙8)x+o(x))/(2∙9∙27x+o(x))) =−((31)/9)](https://www.tinkutara.com/question/Q167595.png)
$$\mathrm{A}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{17}−\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\centerdot\sqrt[{\mathrm{3}}]{\mathrm{3}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{3}} +\mathrm{3}}−\mathrm{9}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{9}−\mathrm{2x}^{\mathrm{2}} −\mathrm{8x}}\centerdot\sqrt[{\mathrm{3}}]{\mathrm{3x}^{\mathrm{3}} +\mathrm{18x}^{\mathrm{2}} +\mathrm{36x}+\mathrm{27}}−\mathrm{9}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\mathrm{9}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}−\frac{\mathrm{8}}{\mathrm{9}}\mathrm{x}−\frac{\mathrm{2}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} }\centerdot\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\mathrm{36}}{\mathrm{27}}\mathrm{x}+\frac{\mathrm{18}}{\mathrm{27}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{27}}\mathrm{x}^{\mathrm{3}} }−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\mathrm{9}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\sqrt{\mathrm{1}−\frac{\mathrm{8}}{\mathrm{9}}\mathrm{x}−\frac{\mathrm{2}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} }\centerdot\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\mathrm{36}}{\mathrm{27}}\mathrm{x}+\frac{\mathrm{18}}{\mathrm{27}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{27}}\mathrm{x}^{\mathrm{3}} }\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\mathrm{9}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{9}}\mathrm{x}−\frac{\mathrm{2}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{36}}{\mathrm{27}}\mathrm{x}+\frac{\mathrm{18}}{\mathrm{27}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{27}}\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\mathrm{9}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2x}}\left[\frac{−\frac{\mathrm{8}}{\mathrm{9}}−\frac{\mathrm{4}}{\mathrm{9}}\mathrm{x}}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{9}}\mathrm{x}−\frac{\mathrm{2}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} \right)}+\frac{\frac{\mathrm{36}}{\mathrm{27}}+\frac{\mathrm{36}}{\mathrm{27}}\mathrm{x}+\frac{\mathrm{9}}{\mathrm{27}}\mathrm{x}^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{36}}{\mathrm{27}}\mathrm{x}+\frac{\mathrm{28}}{\mathrm{27}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{27}}\mathrm{x}^{\mathrm{3}} \right)}\right] \\ $$$$=\mathrm{9}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2x}}\centerdot\left(\frac{−\mathrm{4}−\mathrm{2x}}{\mathrm{9}−\mathrm{8x}−\mathrm{2x}^{\mathrm{2}} }+\frac{\mathrm{12}+\mathrm{12x}+\mathrm{3x}^{\mathrm{2}} }{\mathrm{27}+\mathrm{36x}+\mathrm{28x}^{\mathrm{2}} +\mathrm{3x}^{\mathrm{3}} }\right) \\ $$$$=\mathrm{9}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(−\mathrm{4}−\mathrm{2x}\right)\left(\mathrm{27}+\mathrm{36x}+\mathrm{28x}^{\mathrm{2}} +\mathrm{3x}^{\mathrm{3}} \right)+\left(\mathrm{12}+\mathrm{12x}+\mathrm{3x}^{\mathrm{2}} \right)\left(\mathrm{9}−\mathrm{8x}−\mathrm{2x}^{\mathrm{2}} \right)}{\mathrm{2x}\left(\mathrm{9}−\mathrm{8x}−\mathrm{2x}^{\mathrm{2}} \right)\left(\mathrm{27}+\mathrm{36x}+\mathrm{28x}^{\mathrm{2}} +\mathrm{3x}^{\mathrm{3}} \right)} \\ $$$$=\mathrm{9}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(−\mathrm{4}\centerdot\mathrm{36}−\mathrm{2}\centerdot\mathrm{27}+\mathrm{12}\centerdot\mathrm{9}−\mathrm{12}\centerdot\mathrm{8}\right)\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)}{\mathrm{2}\centerdot\mathrm{9}\centerdot\mathrm{27x}+\mathrm{o}\left(\mathrm{x}\right)} \\ $$$$=−\frac{\mathrm{31}}{\mathrm{9}} \\ $$
Answered by cortano1 last updated on 20/Mar/22
^2 )) A= (1/(18)) lim_(x→2) ((−4x (((3x^3 +3)^2 ))^(1/3) +(17−2x^2 )((2.(9x^2 ))/(3 ((3x^3 +3))^(1/3) )))/(2(x−2))) A=(1/(36)) lim_(x→2) (((((17−2x^2 )6x^2 )/( ((3x^3 +3))^(1/3) )) −4x (((3x^3 +3)^2 ))^(1/3) )/((x−2))) A= (1/(36)) lim_(x→2) (((17−2x^2 )6x^2 −4x(3x^3 +3))/((x−2) ((3x^3 +3))^(1/3) )) A=(1/(108)) lim_(x→2) ((102x^2 −24x^4 −12x)/((x−2))) A= (1/(108)) lim_(x→2) ((204x−96x^3 −12)/1) A= ((408−768−12)/(108)) = − ((31)/9)](https://www.tinkutara.com/question/Q167597.png)
$$\:\mathrm{A}=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\left(\mathrm{17}−\mathrm{2x}^{\mathrm{2}} \right)\sqrt[{\mathrm{3}}]{\left(\mathrm{3x}^{\mathrm{3}} +\mathrm{3}\right)^{\mathrm{2}} }−\mathrm{81}}{\left[\sqrt{\mathrm{17}−\mathrm{2x}^{\mathrm{2}} }\:\sqrt[{\mathrm{3}}]{\mathrm{3x}^{\mathrm{3}} +\mathrm{3}}\:+\mathrm{9}\:\right]\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\mathrm{A}=\:\frac{\mathrm{1}}{\mathrm{18}}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{−\mathrm{4x}\:\sqrt[{\mathrm{3}}]{\left(\mathrm{3x}^{\mathrm{3}} +\mathrm{3}\right)^{\mathrm{2}} }\:+\left(\mathrm{17}−\mathrm{2x}^{\mathrm{2}} \right)\frac{\mathrm{2}.\left(\mathrm{9x}^{\mathrm{2}} \right)}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{3x}^{\mathrm{3}} +\mathrm{3}}}}{\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)} \\ $$$$\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{36}}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\frac{\left(\mathrm{17}−\mathrm{2x}^{\mathrm{2}} \right)\mathrm{6x}^{\mathrm{2}} }{\:\sqrt[{\mathrm{3}}]{\mathrm{3x}^{\mathrm{3}} +\mathrm{3}}}\:−\mathrm{4x}\:\sqrt[{\mathrm{3}}]{\left(\mathrm{3x}^{\mathrm{3}} +\mathrm{3}\right)^{\mathrm{2}} }}{\left(\mathrm{x}−\mathrm{2}\right)} \\ $$$$\:\mathrm{A}=\:\frac{\mathrm{1}}{\mathrm{36}}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\left(\mathrm{17}−\mathrm{2x}^{\mathrm{2}} \right)\mathrm{6x}^{\mathrm{2}} −\mathrm{4x}\left(\mathrm{3x}^{\mathrm{3}} +\mathrm{3}\right)}{\left(\mathrm{x}−\mathrm{2}\right)\:\sqrt[{\mathrm{3}}]{\mathrm{3x}^{\mathrm{3}} +\mathrm{3}}} \\ $$$$\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{108}}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{102x}^{\mathrm{2}} −\mathrm{24x}^{\mathrm{4}} −\mathrm{12x}}{\left(\mathrm{x}−\mathrm{2}\right)} \\ $$$$\:\mathrm{A}=\:\frac{\mathrm{1}}{\mathrm{108}}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{204x}−\mathrm{96x}^{\mathrm{3}} −\mathrm{12}}{\mathrm{1}} \\ $$$$\:\mathrm{A}=\:\frac{\mathrm{408}−\mathrm{768}−\mathrm{12}}{\mathrm{108}}\:=\:−\:\frac{\mathrm{31}}{\mathrm{9}} \\ $$
