Question Number 167647 by mathlove last updated on 22/Mar/22
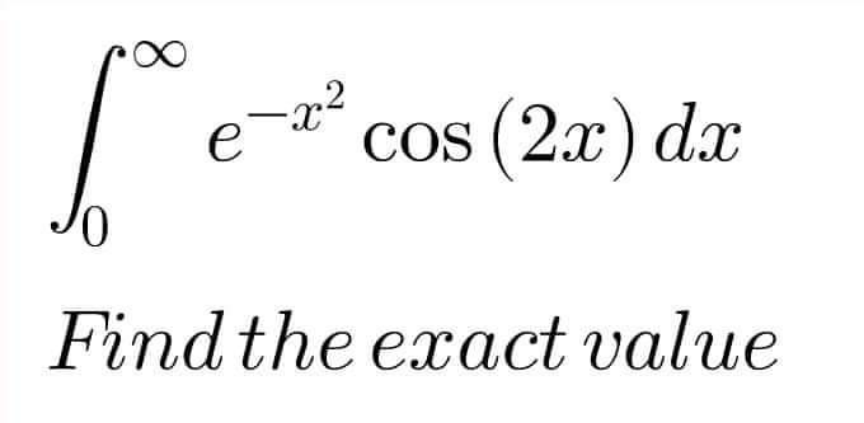
Answered by RoswelCod2003 last updated on 22/Mar/22
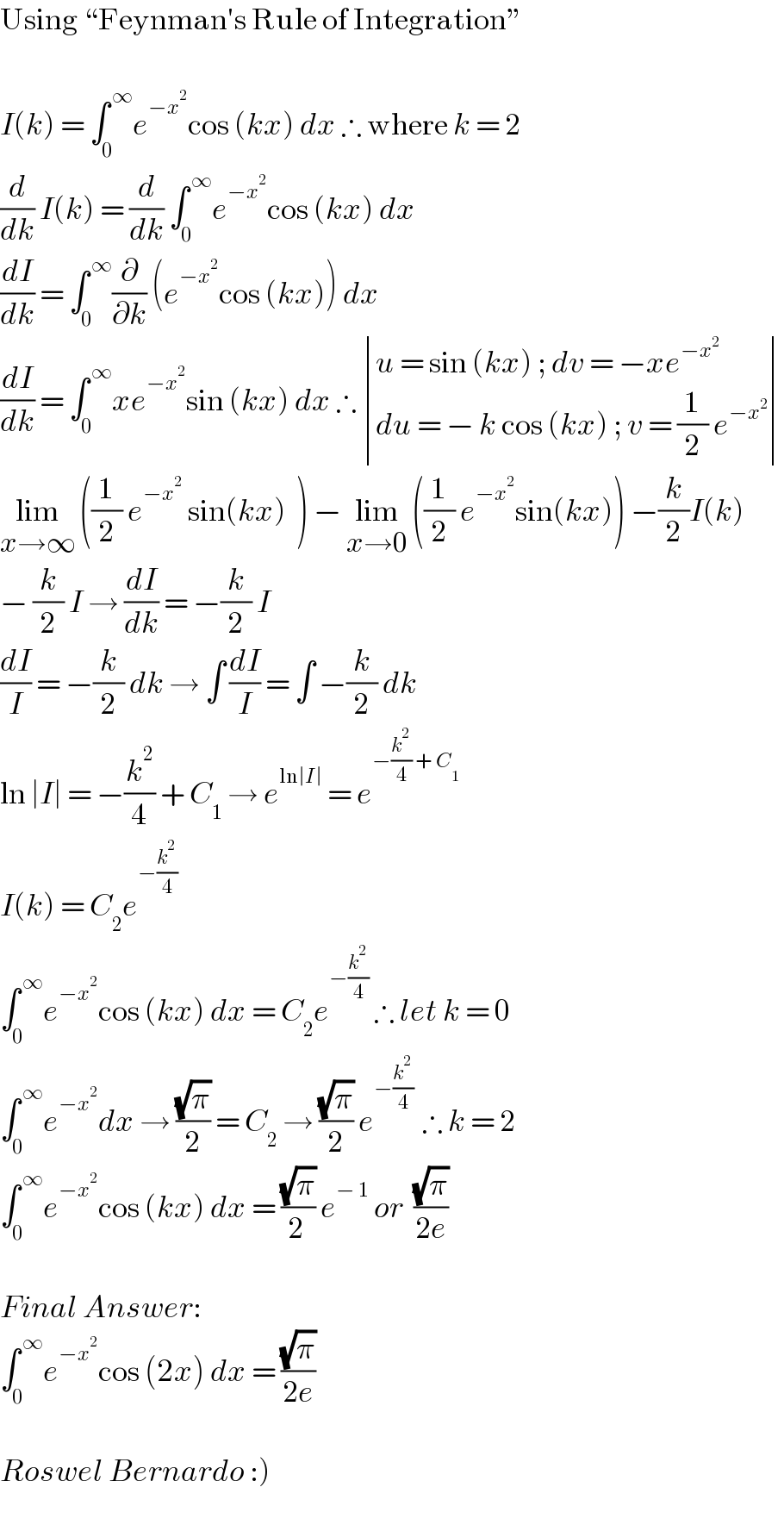
$$\mathrm{Using}\:“\mathrm{Feynman}'\mathrm{s}\:\mathrm{Rule}\:\mathrm{of}\:\mathrm{Integration}'' \\ $$$$\: \\ $$$${I}\left({k}\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}^{\mathrm{2}} } \mathrm{cos}\:\left({kx}\right)\:{dx}\:\therefore\:\mathrm{where}\:{k}\:=\:\mathrm{2} \\ $$$$\frac{{d}}{{dk}}\:{I}\left({k}\right)\:=\:\frac{{d}}{{dk}}\:\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}^{\mathrm{2}} } \mathrm{cos}\:\left({kx}\right)\:{dx} \\ $$$$\frac{{dI}}{{dk}}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\partial}{\partial{k}}\:\left({e}^{−{x}^{\mathrm{2}} } \mathrm{cos}\:\left({kx}\right)\right)\:{dx}\: \\ $$$$\frac{{dI}}{{dk}}\:=\:\int_{\mathrm{0}} ^{\:\infty} {xe}^{−{x}^{\mathrm{2}} } \mathrm{sin}\:\left({kx}\right)\:{dx}\:\therefore\:\begin{vmatrix}{{u}\:=\:\mathrm{sin}\:\left({kx}\right)\:;\:{dv}\:=\:−{xe}^{−{x}^{\mathrm{2}} } }\\{{du}\:=\:−\:{k}\:\mathrm{cos}\:\left({kx}\right)\:;\:{v}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−{x}^{\mathrm{2}} } }\end{vmatrix} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−{x}^{\mathrm{2}} } \:\mathrm{sin}\left({kx}\right)\:\:\right)\:−\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−{x}^{\mathrm{2}} } \mathrm{sin}\left({kx}\right)\right)\:−\frac{{k}}{\mathrm{2}}{I}\left({k}\right) \\ $$$$−\:\frac{{k}}{\mathrm{2}}\:{I}\:\rightarrow\:\frac{{dI}}{{dk}}\:=\:−\frac{{k}}{\mathrm{2}}\:{I} \\ $$$$\frac{{dI}}{{I}}\:=\:−\frac{{k}}{\mathrm{2}}\:{dk}\:\rightarrow\:\int\:\frac{{dI}}{{I}}\:=\:\int\:−\frac{{k}}{\mathrm{2}}\:{dk} \\ $$$$\mathrm{ln}\:\mid{I}\mid\:=\:−\frac{{k}^{\mathrm{2}} }{\mathrm{4}}\:+\:{C}_{\mathrm{1}} \:\rightarrow\:{e}^{\mathrm{ln}\mid{I}\mid} \:=\:{e}^{−\frac{{k}^{\mathrm{2}} }{\mathrm{4}}\:+\:{C}_{\mathrm{1}} } \\ $$$${I}\left({k}\right)\:=\:{C}_{\mathrm{2}} {e}^{−\frac{{k}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}^{\mathrm{2}} } \mathrm{cos}\:\left({kx}\right)\:{dx}\:=\:{C}_{\mathrm{2}} {e}^{−\frac{{k}^{\mathrm{2}} }{\mathrm{4}}} \:\therefore\:{let}\:{k}\:=\:\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}^{\mathrm{2}} } {dx}\:\rightarrow\:\frac{\sqrt{\pi}}{\mathrm{2}}\:=\:{C}_{\mathrm{2}} \:\rightarrow\:\frac{\sqrt{\pi}}{\mathrm{2}}\:{e}^{−\frac{{k}^{\mathrm{2}} }{\mathrm{4}}\:} \:\therefore\:{k}\:=\:\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}^{\mathrm{2}} } \mathrm{cos}\:\left({kx}\right)\:{dx}\:=\:\frac{\sqrt{\pi}}{\mathrm{2}\:}\:{e}^{−\:\mathrm{1}} \:{or}\:\:\frac{\sqrt{\pi}}{\mathrm{2}{e}} \\ $$$$\: \\ $$$${Final}\:{Answer}:\: \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}^{\mathrm{2}} } \mathrm{cos}\:\left(\mathrm{2}{x}\right)\:{dx}\:=\:\frac{\sqrt{\pi}}{\mathrm{2}{e}} \\ $$$$\: \\ $$$$\left.{Roswel}\:{Bernardo}\::\right) \\ $$$$\: \\ $$
Commented by mkam last updated on 22/Mar/22
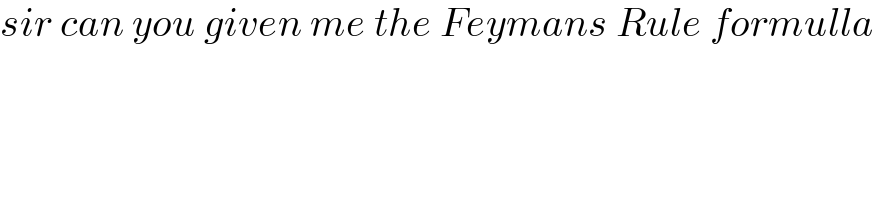
$${sir}\:{can}\:{you}\:{given}\:{me}\:{the}\:{Feymans}\:{Rule}\:{formulla} \\ $$
Commented by mkam last updated on 22/Mar/22
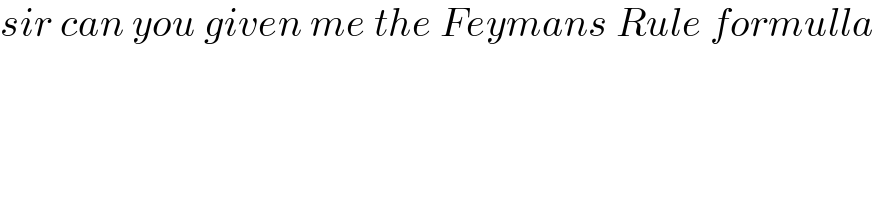
$${sir}\:{can}\:{you}\:{given}\:{me}\:{the}\:{Feymans}\:{Rule}\:{formulla} \\ $$
Commented by RoswelCod2003 last updated on 22/Mar/22
![Ahmmm... The Feynman′s Rule or Feynman′s Trick is performed by differentiating undwr the integral sign. Example: ∫_(−1) ^( 1) (2kx + k^2 ) dx set this integral as function of any variable, let′s “k” F(k) = ∫_(−1) ^( 1) (2kx + k^2 ) dx get the derivative both sides with respect to k (d/dk) F(k) = (d/dk)∫_(−1) ^( 1) (2kx + k^2 ) dx ∴ the derivative of F(k) is simply F ′(k) or (dF/dk) (dF/dk) = (d/dk) ∫_(−1) ^( 1) (2kx + k^2 ) dx ∴ before you get the derivative of (2kx + k^2 ) put first the derivative notion inside the integral sign but transform it into partial derivative notation: (dF/dk) = ∫_(−1) ^( 1) (∂/∂k)(2kx + k^2 ) dx ∴ then the derivative of the function under the integral sign. we will have: (dF/dk) = ∫_(−1) ^( 1) (2x + 2k) dx ∴ now integrate with respect to X: (dF/dk) = ((2x^(1+1) )/(1+1)) → ((2x^2 )/2) = x^2 + 2k 2k will remain to 2k because we are integrating with respect to x not k we will have: [x^2 + 2k]_(−1) ^1 apply now the fundamental theorem of calculus ∫_a ^( b) f(x) dx = f(b) − f(a) [f(b) = (x^2 + 2k)] − [f(a) = (x^2 + 2k)] [f(1) = (1 + 2k)] −[f(−1) = (1 + 2k)] 1 + 2k − 1 + 2k = 4k Final Answer: ∫_(−1) ^( 1) (2kx + k^2 ) dx = 4k hope you learned something, you can actually learn this from youtube:) Roswel Bernardo at your service <3](https://www.tinkutara.com/question/Q167658.png)
$$\: \\ $$$${Ahmmm}…\:{The}\:{Feynman}'{s}\:{Rule}\:{or}\:{Feynman}'{s}\:{Trick} \\ $$$${is}\:{performed}\:{by}\:{differentiating}\:{undwr}\:{the}\:{integral}\:{sign}.\: \\ $$$$\: \\ $$$$\mathrm{E}{xample}: \\ $$$$\: \\ $$$$\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left(\mathrm{2}{kx}\:+\:{k}^{\mathrm{2}} \right)\:{dx} \\ $$$${set}\:{this}\:{integral}\:{as}\:{function}\:{of}\:{any}\:{variable},\:{let}'{s}\:“{k}'' \\ $$$${F}\left({k}\right)\:=\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left(\mathrm{2}{kx}\:+\:{k}^{\mathrm{2}} \right)\:{dx} \\ $$$${get}\:{the}\:{derivative}\:{both}\:{sides}\:{with}\:{respect}\:{to}\:{k} \\ $$$$ \\ $$$$\frac{{d}}{{dk}}\:{F}\left({k}\right)\:=\:\frac{{d}}{{dk}}\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left(\mathrm{2}{kx}\:+\:{k}^{\mathrm{2}} \right)\:{dx}\:\therefore\:{the}\:{derivative}\:{of}\:{F}\left({k}\right)\:{is}\:{simply}\:{F}\:'\left({k}\right)\:{or}\:\frac{{dF}}{{dk}} \\ $$$$\frac{{dF}}{{dk}}\:=\:\frac{{d}}{{dk}}\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left(\mathrm{2}{kx}\:+\:{k}^{\mathrm{2}} \right)\:{dx}\:\therefore\:{before}\:{you}\:{get}\:{the}\:{derivative}\:{of}\:\left(\mathrm{2}{kx}\:+\:{k}^{\mathrm{2}} \right) \\ $$$${put}\:{first}\:{the}\:{derivative}\:{notion}\:{inside}\:{the}\:{integral}\:{sign}\:{but}\:{transform}\:{it} \\ $$$${into}\:\boldsymbol{\mathrm{partial}}\:\boldsymbol{\mathrm{derivative}}\:\boldsymbol{\mathrm{notation}}: \\ $$$$\: \\ $$$$\frac{{dF}}{{dk}}\:=\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} \frac{\partial}{\partial{k}}\left(\mathrm{2}{kx}\:+\:{k}^{\mathrm{2}} \right)\:{dx}\:\therefore\:{then}\:{the}\:{derivative}\:{of}\:{the}\:{function}\:{under}\:{the} \\ $$$${integral}\:{sign}. \\ $$$$\: \\ $$$${we}\:{will}\:{have}:\:\frac{{dF}}{{dk}}\:=\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left(\mathrm{2}{x}\:+\:\mathrm{2}{k}\right)\:{dx}\:\therefore\:{now}\:{integrate}\:{with} \\ $$$${respect}\:{to}\:{X}: \\ $$$$\: \\ $$$$\frac{{dF}}{{dk}}\:=\:\:\frac{\mathrm{2}{x}^{\mathrm{1}+\mathrm{1}} }{\mathrm{1}+\mathrm{1}}\:\rightarrow\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}}\:=\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{k} \\ $$$$\: \\ $$$$ \\ $$$$\mathrm{2}{k}\:{will}\:{remain}\:{to}\:\mathrm{2}{k}\:{because}\:{we}\:{are}\:{integrating} \\ $$$${with}\:{respect}\:{to}\:{x}\:{not}\:{k} \\ $$$$\: \\ $$$${we}\:{will}\:{have}:\:\left[{x}^{\mathrm{2}} \:+\:\mathrm{2}{k}\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$${apply}\:{now}\:{the}\:{fundamental}\:{theorem}\:{of}\:{calculus} \\ $$$$\: \\ $$$$\int_{{a}} ^{\:{b}} {f}\left({x}\right)\:{dx}\:\:=\:{f}\left({b}\right)\:−\:{f}\left({a}\right) \\ $$$$\left[{f}\left({b}\right)\:=\:\:\left({x}^{\mathrm{2}} \:+\:\mathrm{2}{k}\right)\right]\:−\:\left[{f}\left({a}\right)\:=\:\left({x}^{\mathrm{2}} \:+\:\mathrm{2}{k}\right)\right] \\ $$$$\left[{f}\left(\mathrm{1}\right)\:=\:\left(\mathrm{1}\:+\:\mathrm{2}{k}\right)\right]\:−\left[{f}\left(−\mathrm{1}\right)\:=\:\left(\mathrm{1}\:+\:\mathrm{2}{k}\right)\right] \\ $$$$\mathrm{1}\:+\:\mathrm{2}{k}\:−\:\mathrm{1}\:+\:\mathrm{2}{k}\:=\:\mathrm{4}{k} \\ $$$$\: \\ $$$$\mathrm{Final}\:\mathrm{Answer}:\: \\ $$$$\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left(\mathrm{2}{kx}\:+\:{k}^{\mathrm{2}} \right)\:{dx}\:=\:\mathrm{4}{k} \\ $$$$\: \\ $$$${hope}\:{you}\:{learned}\:{something},\:{you}\:{can}\:{actually}\: \\ $$$$\left.{learn}\:{this}\:{from}\:{youtube}:\right) \\ $$$$\: \\ $$$$\mathrm{Roswel}\:\mathrm{Bernardo}\:\mathrm{at}\:\mathrm{your}\:\mathrm{service}\:<\mathrm{3} \\ $$
Answered by Mathspace last updated on 22/Mar/22
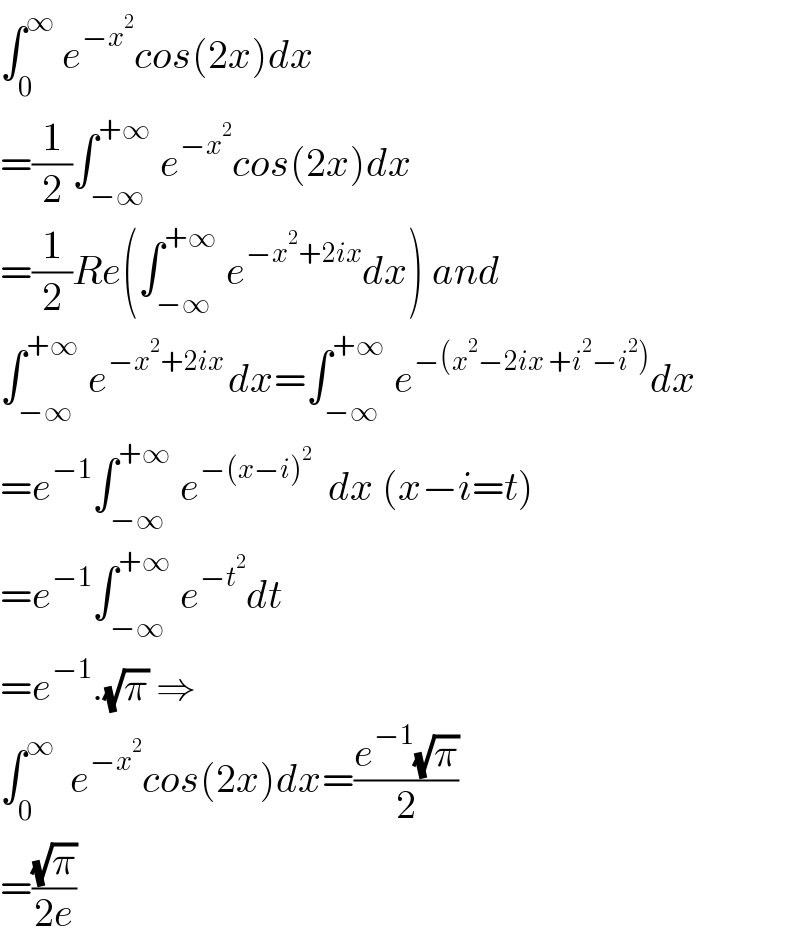
$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{2}} } {cos}\left(\mathrm{2}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } {cos}\left(\mathrm{2}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} +\mathrm{2}{ix}} {dx}\right)\:{and} \\ $$$$\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} +\mathrm{2}{ix}\:} {dx}=\int_{−\infty} ^{+\infty} \:{e}^{−\left({x}^{\mathrm{2}} −\mathrm{2}{ix}\:+{i}^{\mathrm{2}} −{i}^{\mathrm{2}} \right)} {dx} \\ $$$$={e}^{−\mathrm{1}} \int_{−\infty} ^{+\infty} \:{e}^{−\left({x}−{i}\right)^{\mathrm{2}} } \:\:{dx}\:\left({x}−{i}={t}\right) \\ $$$$={e}^{−\mathrm{1}} \int_{−\infty} ^{+\infty} \:{e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$={e}^{−\mathrm{1}} .\sqrt{\pi}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}^{\mathrm{2}} } {cos}\left(\mathrm{2}{x}\right){dx}=\frac{{e}^{−\mathrm{1}} \sqrt{\pi}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}{e}} \\ $$
