Question Number 167690 by peter frank last updated on 22/Mar/22

Answered by som(math1967) last updated on 23/Mar/22
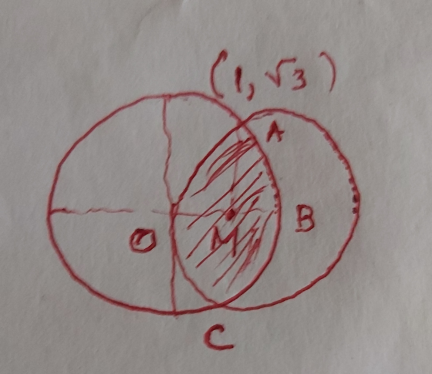
![by solving x^2 +y^2 =4 and (x−2)^2 +y^2 =4 x=1 ,y=±(√3) area of OABCO =2×areaOMBAO =2×2MBAM =4∫_1 ^2 (√(4−x^2 ))dx =4[((x(√(4−x^2 )))/2) +(4/2)sin^(−1) (x/2)]_1 ^2 =4[2sin^(−1) 1−((√3)/2) −2sin^(−1) (1/2)] =4[π−(π/3)−((√3)/2)] =(((8π)/3)−2(√3))sq unit](https://www.tinkutara.com/question/Q167693.png)
$${by}\:{solving}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}\:{and}\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4} \\ $$$${x}=\mathrm{1}\:,{y}=\pm\sqrt{\mathrm{3}} \\ $$$${area}\:{of}\:{OABCO} \\ $$$$=\mathrm{2}×{areaOMBAO} \\ $$$$=\mathrm{2}×\mathrm{2}{MBAM} \\ $$$$=\mathrm{4}\int_{\mathrm{1}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{4}\left[\frac{{x}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{\mathrm{2}}\:+\frac{\mathrm{4}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\mathrm{4}\left[\mathrm{2sin}^{−\mathrm{1}} \mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:−\mathrm{2sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$$$=\mathrm{4}\left[\pi−\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right] \\ $$$$=\left(\frac{\mathrm{8}\pi}{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{3}}\right){sq}\:{unit} \\ $$
Commented by som(math1967) last updated on 23/Mar/22