Question Number 16771 by Tinkutara last updated on 26/Jun/17
Commented by Tinkutara last updated on 26/Jun/17

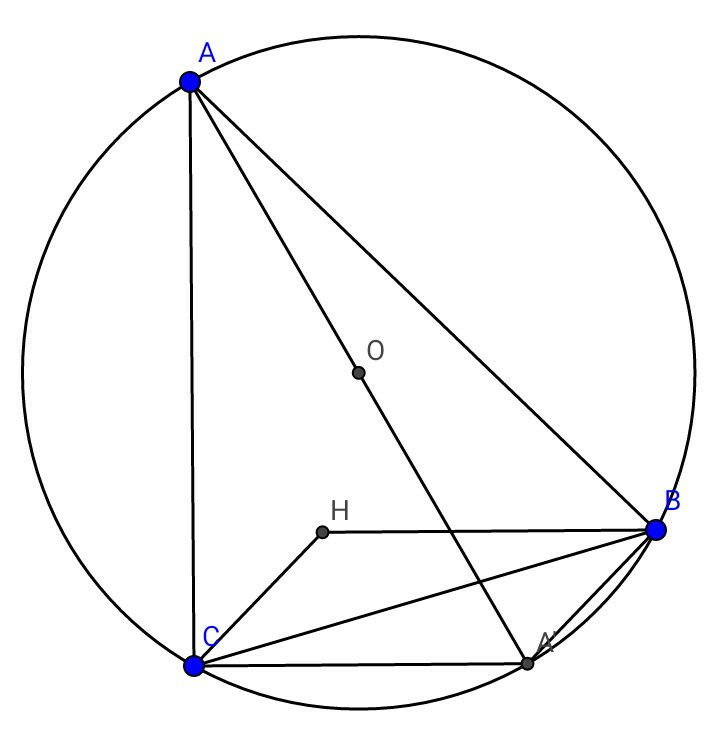
$$\left(\mathrm{1}\right)\:{O}\:\mathrm{is}\:\mathrm{circumcenter}\:\mathrm{and}\:{H}\:\mathrm{is}\:\mathrm{orthocenter} \\ $$$$\mathrm{of}\:\Delta{ABC}.\:{AOA}'\:\mathrm{is}\:\mathrm{the}\:\mathrm{diameter}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:{A}'{BHC}\:\mathrm{is}\:\mathrm{a}\:\mathrm{parallelogram}. \\ $$
Answered by ajfour last updated on 26/Jun/17

$$\mathrm{CH}\:\mathrm{and}\:\mathrm{A}'\mathrm{B}\:\bot\:\mathrm{to}\:\mathrm{AB}\:\mathrm{hence}\:\mathrm{parallel} \\ $$$$\mathrm{BH}\:\mathrm{and}\:\mathrm{A}'\mathrm{C}\:\bot\:\mathrm{to}\:\mathrm{AC}\:\mathrm{hence}\:\mathrm{parallel}. \\ $$$$\:\mathrm{A}'\mathrm{BHC}\:\mathrm{is}\:\mathrm{thus}\:\mathrm{a}\:\mathrm{parallelogram}. \\ $$
Commented by Tinkutara last updated on 26/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 26/Jun/17
Commented by ajfour last updated on 26/Jun/17

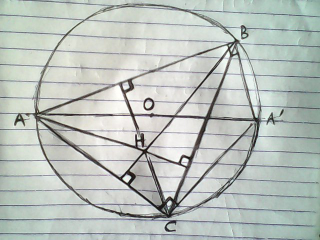
$$\overset{\rightarrow} {\mathrm{HA}}+\overset{\rightarrow} {\mathrm{HA}}'\neq\:\overset{\rightarrow} {\mathrm{HO}}\:\:\left(\mathrm{O}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{AA}'\right). \\ $$
Commented by Tinkutara last updated on 26/Jun/17

$$\overset{\rightarrow} {{HA}'}\:+\:\overset{\rightarrow} {{HA}}\:\mathrm{will}\:\mathrm{be}\:\overset{\rightarrow} {{HO}}\:\mathrm{or}\:\mathrm{2}\overset{\rightarrow} {{HO}}?\:\mathrm{I} \\ $$$$\mathrm{proved}\:\mathrm{it}\:\mathrm{2}\overset{\rightarrow} {{HO}}\:\mathrm{but}\:\mathrm{my}\:\mathrm{book}\:\mathrm{says}\:\mathrm{it} \\ $$$$\overset{\rightarrow} {{HO}}.\:\mathrm{Please}\:\mathrm{only}\:\mathrm{mention}\:\mathrm{the}\:\mathrm{answer} \\ $$$$\mathrm{if}\:\mathrm{I}\:\mathrm{am}\:\mathrm{right}. \\ $$
