Question Number 167775 by peter frank last updated on 24/Mar/22
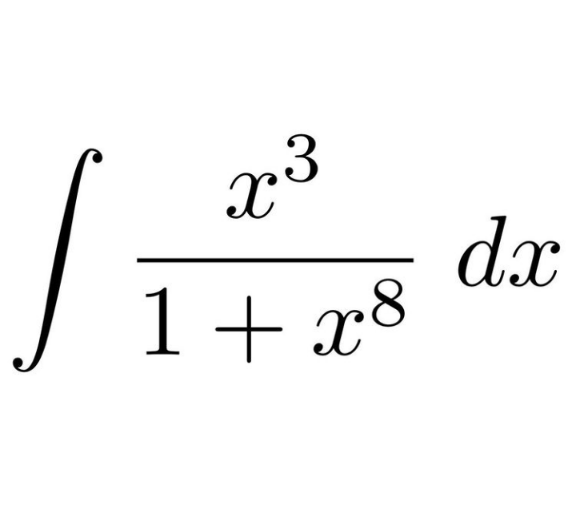
Commented by infinityaction last updated on 24/Mar/22

$${put}\:{x}^{\mathrm{4}\:} \:={t} \\ $$
Answered by peter frank last updated on 25/Mar/22
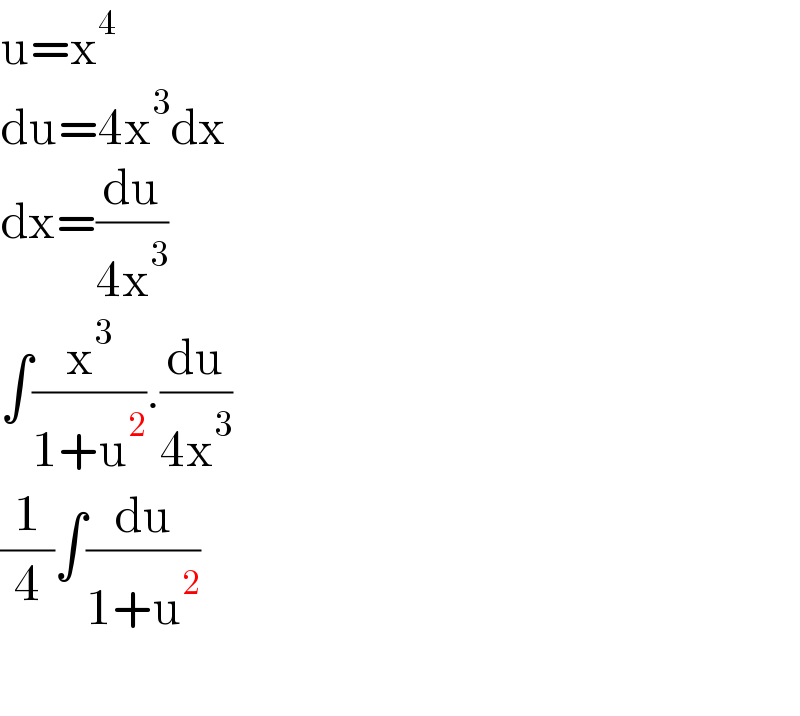
$$\mathrm{u}=\mathrm{x}^{\mathrm{4}} \\ $$$$\mathrm{du}=\mathrm{4x}^{\mathrm{3}} \mathrm{dx} \\ $$$$\mathrm{dx}=\frac{\mathrm{du}}{\mathrm{4x}^{\mathrm{3}} } \\ $$$$\int\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }.\frac{\mathrm{du}}{\mathrm{4x}^{\mathrm{3}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by mr W last updated on 25/Mar/22
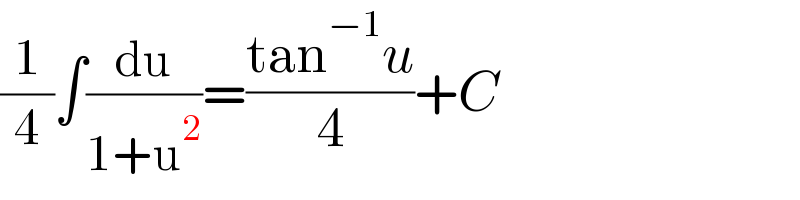
$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }=\frac{\mathrm{tan}^{−\mathrm{1}} {u}}{\mathrm{4}}+{C} \\ $$
Commented by peter frank last updated on 25/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
