Question Number 167777 by infinityaction last updated on 24/Mar/22
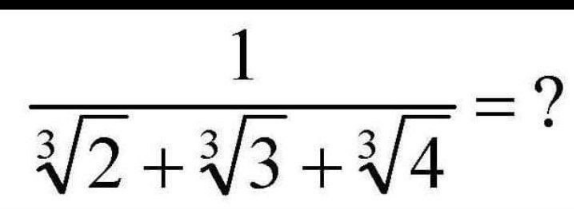
Answered by Jamshidbek last updated on 26/Mar/22
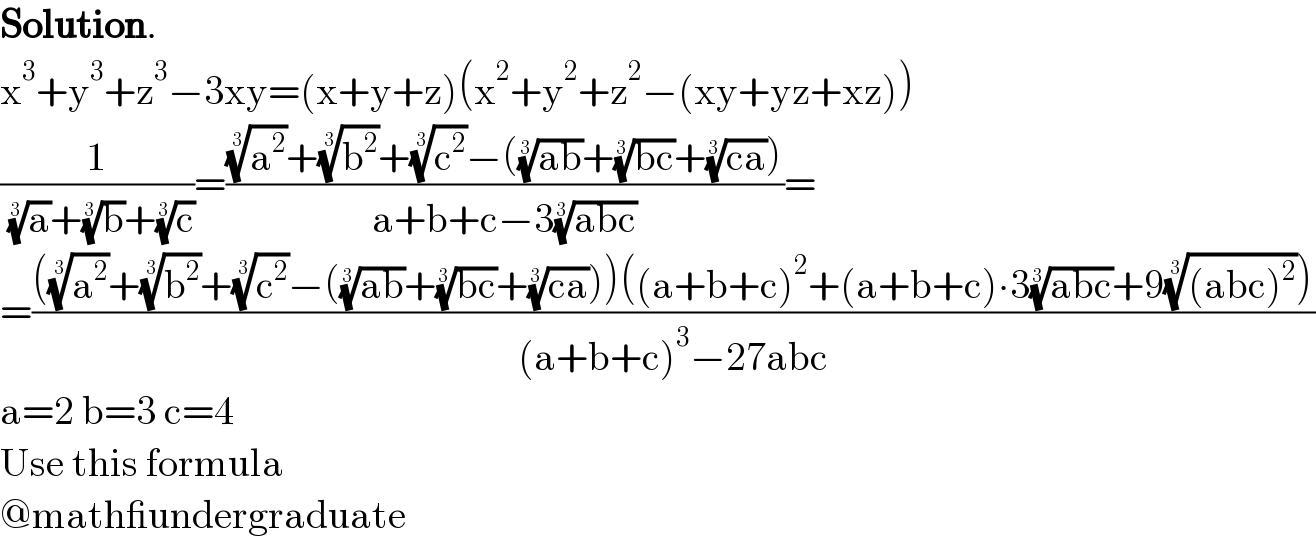
$$\boldsymbol{\mathrm{Solution}}. \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +\mathrm{z}^{\mathrm{3}} −\mathrm{3xy}=\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} −\left(\mathrm{xy}+\mathrm{yz}+\mathrm{xz}\right)\right) \\ $$$$\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{a}}+\sqrt[{\mathrm{3}}]{\mathrm{b}}+\sqrt[{\mathrm{3}}]{\mathrm{c}}}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{a}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\mathrm{b}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\mathrm{c}^{\mathrm{2}} }−\left(\sqrt[{\mathrm{3}}]{\mathrm{ab}}+\sqrt[{\mathrm{3}}]{\mathrm{bc}}+\sqrt[{\mathrm{3}}]{\mathrm{ca}}\right)}{\mathrm{a}+\mathrm{b}+\mathrm{c}−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{abc}}}= \\ $$$$=\frac{\left(\sqrt[{\mathrm{3}}]{\mathrm{a}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\mathrm{b}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\mathrm{c}^{\mathrm{2}} }−\left(\sqrt[{\mathrm{3}}]{\mathrm{ab}}+\sqrt[{\mathrm{3}}]{\mathrm{bc}}+\sqrt[{\mathrm{3}}]{\mathrm{ca}}\right)\right)\left(\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)^{\mathrm{2}} +\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\centerdot\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{abc}}+\mathrm{9}\sqrt[{\mathrm{3}}]{\left(\mathrm{abc}\right)^{\mathrm{2}} }\right)}{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)^{\mathrm{3}} −\mathrm{27abc}} \\ $$$$\mathrm{a}=\mathrm{2}\:\mathrm{b}=\mathrm{3}\:\mathrm{c}=\mathrm{4} \\ $$$$\mathrm{Use}\:\mathrm{this}\:\mathrm{formula} \\ $$$$@\mathrm{math\_undergraduate} \\ $$
