Question Number 167823 by cortano1 last updated on 26/Mar/22

Commented by dangduomg last updated on 26/Mar/22
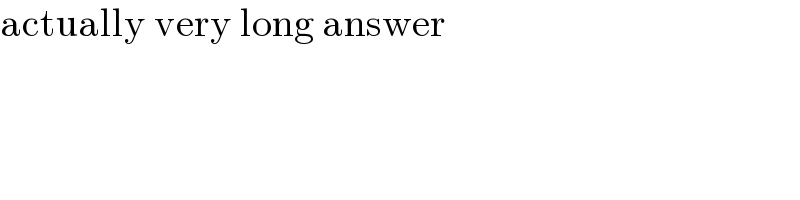
$$\mathrm{actually}\:\mathrm{very}\:\mathrm{long}\:\mathrm{answer} \\ $$
Commented by MJS_new last updated on 26/Mar/22
![a first steps ∫((ln (1+(√(x^2 −(1/3)))))/(x(√(x^2 −(1/3)))))dx= [t=1+(√(x^2 −(1/3))) → dx=((√(x^2 −(1/3)))/x)dt] =∫((ln t)/(t^2 −2t+(4/3)))dt= =∫((ln t)/((t−1−((√3)/3)i)(t−1+((√3)/3)i)))dt=... this can be solved but it takes some time... ((ln t)/((t−a)(t−b)))=((ln t)/((a−b)(t−a)))+((ln t)/((b−a)(t−b))) ...](https://www.tinkutara.com/question/Q167826.png)
$$\mathrm{a}\:\mathrm{first}\:\mathrm{steps} \\ $$$$\int\frac{\mathrm{ln}\:\left(\mathrm{1}+\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}\right)}{{x}\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{1}+\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}}{{x}}{dt}\right] \\ $$$$=\int\frac{\mathrm{ln}\:{t}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\frac{\mathrm{4}}{\mathrm{3}}}{dt}= \\ $$$$=\int\frac{\mathrm{ln}\:{t}}{\left({t}−\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{i}\right)\left({t}−\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{i}\right)}{dt}=… \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{but}\:\mathrm{it}\:\mathrm{takes}\:\mathrm{some}\:\mathrm{time}… \\ $$$$\frac{\mathrm{ln}\:{t}}{\left({t}−{a}\right)\left({t}−{b}\right)}=\frac{\mathrm{ln}\:{t}}{\left({a}−{b}\right)\left({t}−{a}\right)}+\frac{\mathrm{ln}\:{t}}{\left({b}−{a}\right)\left({t}−{b}\right)} \\ $$$$… \\ $$
Answered by Mathspace last updated on 27/Mar/22
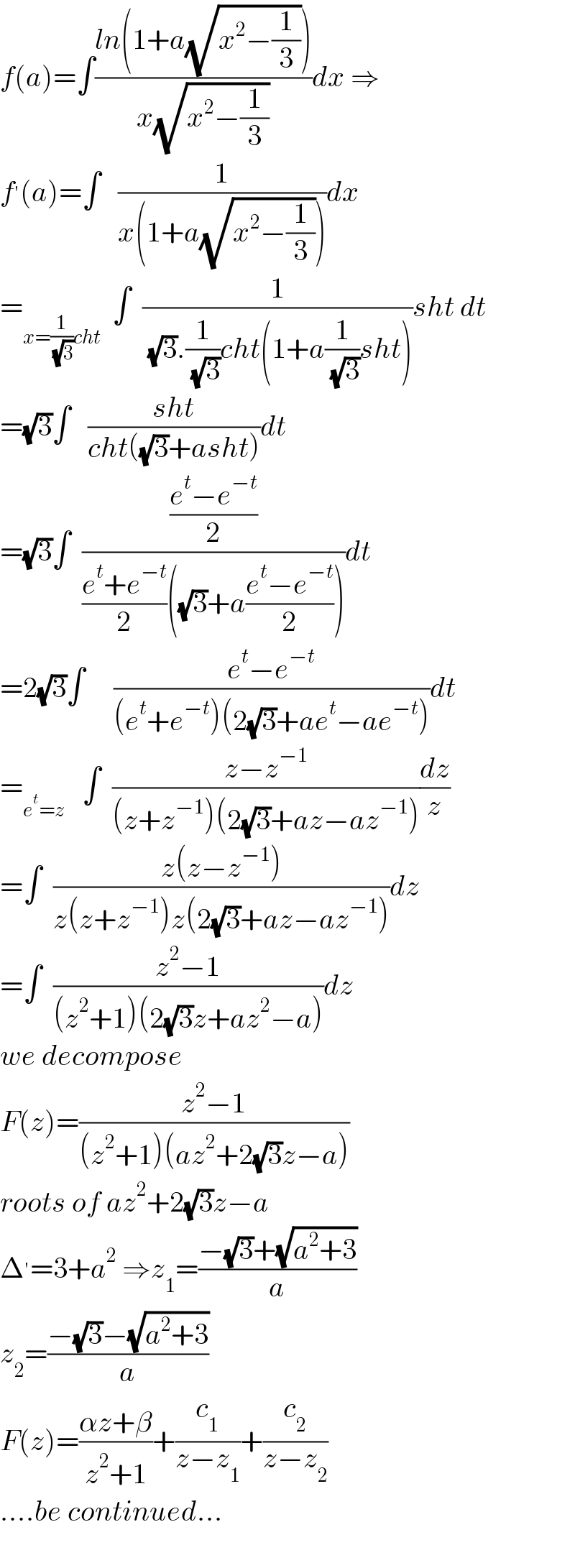
$${f}\left({a}\right)=\int\frac{{ln}\left(\mathrm{1}+{a}\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}\right)}{{x}\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}}{dx}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)=\int\:\:\:\frac{\mathrm{1}}{{x}\left(\mathrm{1}+{a}\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}}\right)}{dx} \\ $$$$=_{{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{cht}} \:\:\int\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{cht}\left(\mathrm{1}+{a}\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sht}\right)}{sht}\:{dt} \\ $$$$=\sqrt{\mathrm{3}}\int\:\:\:\frac{{sht}}{{cht}\left(\sqrt{\mathrm{3}}+{asht}\right)}{dt} \\ $$$$=\sqrt{\mathrm{3}}\int\:\:\frac{\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}}{\frac{{e}^{{t}} +{e}^{−{t}} }{\mathrm{2}}\left(\sqrt{\mathrm{3}}+{a}\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}\right)}{dt} \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\int\:\:\:\:\:\frac{{e}^{{t}} −{e}^{−{t}} }{\left({e}^{{t}} +{e}^{−{t}} \right)\left(\mathrm{2}\sqrt{\mathrm{3}}+{ae}^{{t}} −{ae}^{−{t}} \right)}{dt} \\ $$$$=_{{e}^{{t}} ={z}} \:\:\:\int\:\:\frac{{z}−{z}^{−\mathrm{1}} }{\left({z}+{z}^{−\mathrm{1}} \right)\left(\mathrm{2}\sqrt{\mathrm{3}}+{az}−{az}^{−\mathrm{1}} \right)}\frac{{dz}}{{z}} \\ $$$$=\int\:\:\frac{{z}\left({z}−{z}^{−\mathrm{1}} \right)}{{z}\left({z}+{z}^{−\mathrm{1}} \right){z}\left(\mathrm{2}\sqrt{\mathrm{3}}+{az}−{az}^{−\mathrm{1}} \right)}{dz} \\ $$$$=\int\:\:\frac{{z}^{\mathrm{2}} −\mathrm{1}}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{3}}{z}+{az}^{\mathrm{2}} −{a}\right)}{dz} \\ $$$${we}\:{decompose} \\ $$$${F}\left({z}\right)=\frac{{z}^{\mathrm{2}} −\mathrm{1}}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)\left({az}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{z}−{a}\right)} \\ $$$${roots}\:{of}\:{az}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{z}−{a} \\ $$$$\Delta^{'} =\mathrm{3}+{a}^{\mathrm{2}} \:\Rightarrow{z}_{\mathrm{1}} =\frac{−\sqrt{\mathrm{3}}+\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}}{{a}} \\ $$$${z}_{\mathrm{2}} =\frac{−\sqrt{\mathrm{3}}−\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}}{{a}} \\ $$$${F}\left({z}\right)=\frac{\alpha{z}+\beta}{{z}^{\mathrm{2}} +\mathrm{1}}+\frac{{c}_{\mathrm{1}} }{{z}−{z}_{\mathrm{1}} }+\frac{{c}_{\mathrm{2}} }{{z}−{z}_{\mathrm{2}} } \\ $$$$….{be}\:{continued}… \\ $$$$ \\ $$
