Question-167964

Question Number 167964 by mnjuly1970 last updated on 30/Mar/22

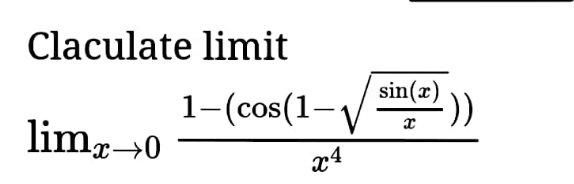
Commented by greogoury55 last updated on 30/Mar/22

= lim_(x→0) ((1−cos ((((√x)−(√(sin x)))/( (√x)))))/x^4 ) = lim_(x→0) ((2sin^2 ((((√x)−(√(sin x)))/(2(√x)))))/x^4 ) =(1/2)lim_(x→0) ((((√x)−(√(sin x)))/(x^2 (√x))))^2 =(1/2)[lim_(x→0) ((x−sin x)/x^3 ) .lim_(x→0) ((√x)/( (√x)+(√(sin x)))) ]^2 =(1/2)[(1/6).lim_(x→0) (1/(1+(√((sin x)/x)))) ]^2 =(1/2)×(1/(144)) = (1/(288))

$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\left(\frac{\sqrt{{x}}−\sqrt{\mathrm{sin}\:{x}}}{\:\sqrt{{x}}}\right)}{{x}^{\mathrm{4}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}^{\mathrm{2}} \:\left(\frac{\sqrt{{x}}−\sqrt{\mathrm{sin}\:{x}}}{\mathrm{2}\sqrt{{x}}}\right)}{{x}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\sqrt{{x}}−\sqrt{\mathrm{sin}\:{x}}}{{x}^{\mathrm{2}} \sqrt{{x}}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\:.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}}}{\:\sqrt{{x}}+\sqrt{\mathrm{sin}\:{x}}}\:\right]^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{6}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\frac{\mathrm{sin}\:{x}}{{x}}}}\:\right]^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{144}}\:=\:\frac{\mathrm{1}}{\mathrm{288}} \\ $$

Answered by qaz last updated on 30/Mar/22

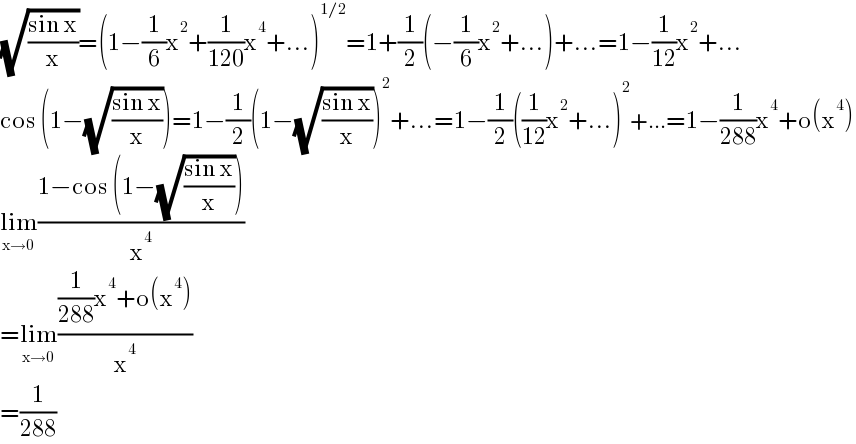
(√((sin x)/x))=(1−(1/6)x^2 +(1/(120))x^4 +...)^(1/2) =1+(1/2)(−(1/6)x^2 +...)+...=1−(1/(12))x^2 +... cos (1−(√((sin x)/x)))=1−(1/2)(1−(√((sin x)/x)))^2 +...=1−(1/2)((1/(12))x^2 +...)^2 +...=1−(1/(288))x^4 +o(x^4 ) lim_(x→0) ((1−cos (1−(√((sin x)/x))))/x^4 ) =lim_(x→0) (((1/(288))x^4 +o(x^4 ))/x^4 ) =(1/(288))

$$\sqrt{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{120}}\mathrm{x}^{\mathrm{4}} +…\right)^{\mathrm{1}/\mathrm{2}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} +…\right)+…=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{x}^{\mathrm{2}} +… \\ $$$$\mathrm{cos}\:\left(\mathrm{1}−\sqrt{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}}\right)^{\mathrm{2}} +…=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{12}}\mathrm{x}^{\mathrm{2}} +…\right)^{\mathrm{2}} +…=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{288}}\mathrm{x}^{\mathrm{4}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right) \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{1}−\sqrt{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}}\right)}{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{288}}\mathrm{x}^{\mathrm{4}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{288}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply