Question Number 168094 by cortano1 last updated on 03/Apr/22
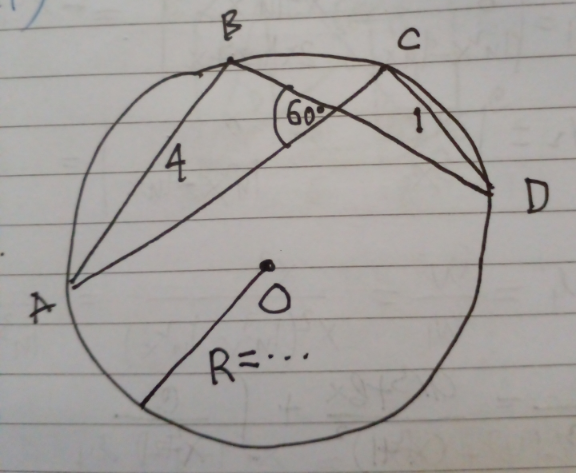
Answered by mr W last updated on 03/Apr/22
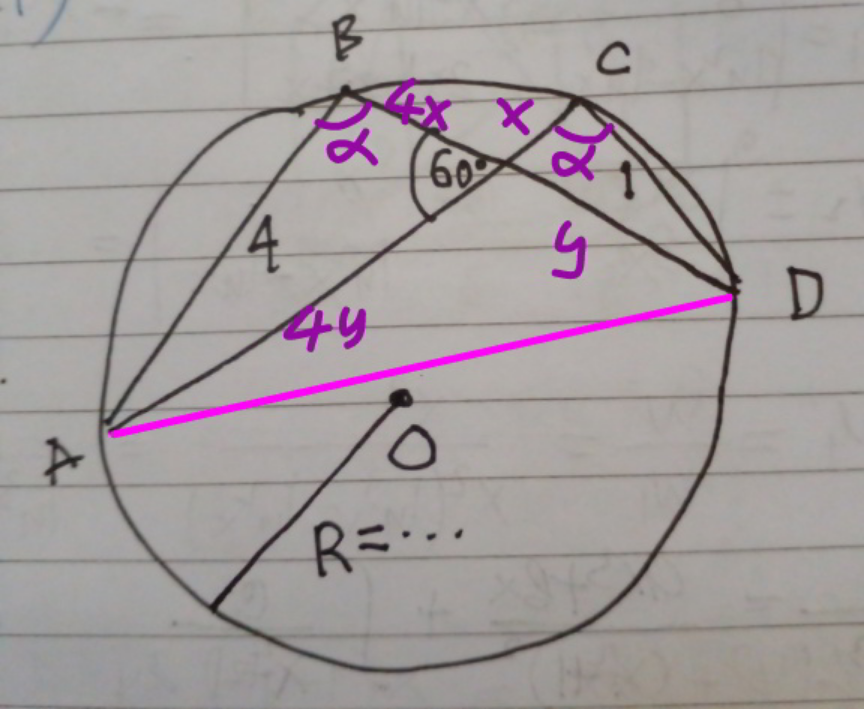
Commented by mr W last updated on 03/Apr/22
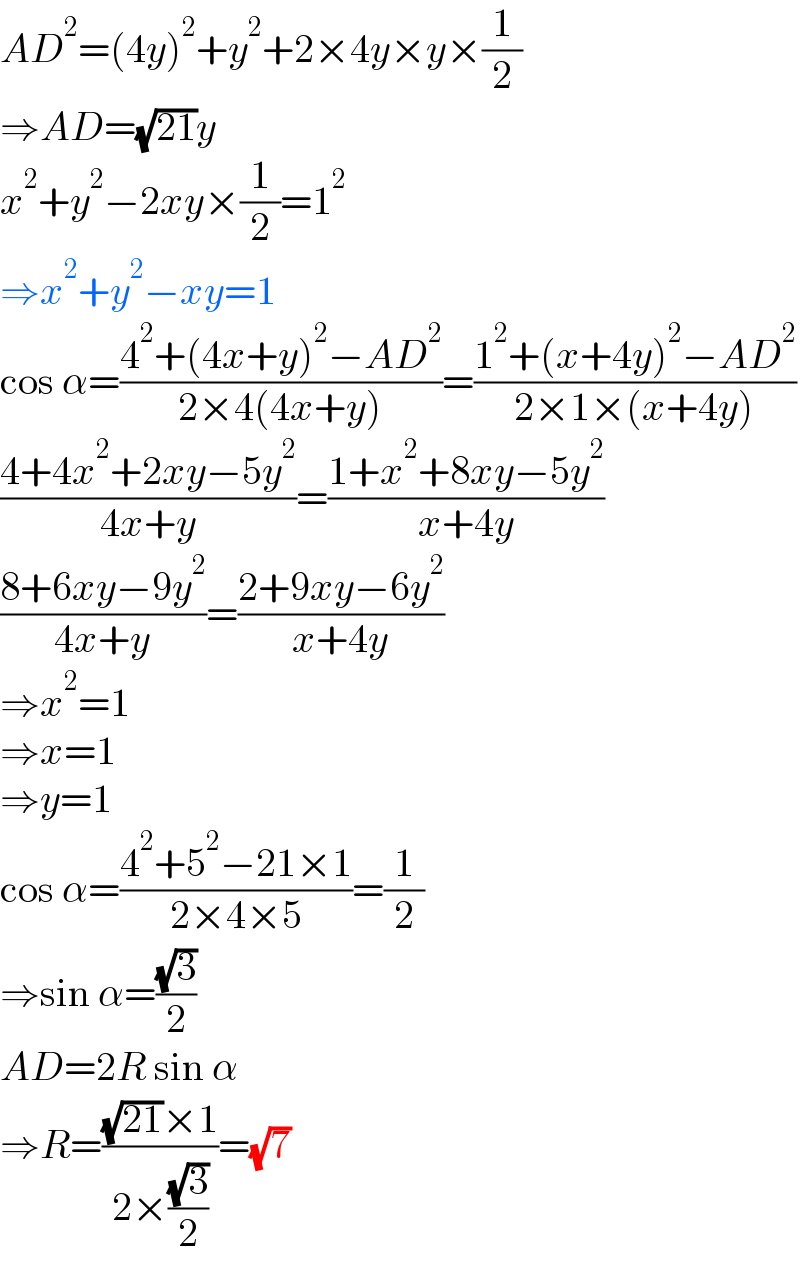
$${AD}^{\mathrm{2}} =\left(\mathrm{4}{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}×\mathrm{4}{y}×{y}×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{AD}=\sqrt{\mathrm{21}}{y} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}×\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{xy}=\mathrm{1} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{4}^{\mathrm{2}} +\left(\mathrm{4}{x}+{y}\right)^{\mathrm{2}} −{AD}^{\mathrm{2}} }{\mathrm{2}×\mathrm{4}\left(\mathrm{4}{x}+{y}\right)}=\frac{\mathrm{1}^{\mathrm{2}} +\left({x}+\mathrm{4}{y}\right)^{\mathrm{2}} −{AD}^{\mathrm{2}} }{\mathrm{2}×\mathrm{1}×\left({x}+\mathrm{4}{y}\right)} \\ $$$$\frac{\mathrm{4}+\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}{xy}−\mathrm{5}{y}^{\mathrm{2}} }{\mathrm{4}{x}+{y}}=\frac{\mathrm{1}+{x}^{\mathrm{2}} +\mathrm{8}{xy}−\mathrm{5}{y}^{\mathrm{2}} }{{x}+\mathrm{4}{y}} \\ $$$$\frac{\mathrm{8}+\mathrm{6}{xy}−\mathrm{9}{y}^{\mathrm{2}} }{\mathrm{4}{x}+{y}}=\frac{\mathrm{2}+\mathrm{9}{xy}−\mathrm{6}{y}^{\mathrm{2}} }{{x}+\mathrm{4}{y}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{1} \\ $$$$\Rightarrow{y}=\mathrm{1} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{21}×\mathrm{1}}{\mathrm{2}×\mathrm{4}×\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${AD}=\mathrm{2}{R}\:\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{R}=\frac{\sqrt{\mathrm{21}}×\mathrm{1}}{\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\sqrt{\mathrm{7}} \\ $$
Commented by Tawa11 last updated on 03/Apr/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
