Question Number 168180 by peter frank last updated on 05/Apr/22

Answered by MJS_new last updated on 05/Apr/22

$$\left(\mathrm{i}\right)\:\mathrm{if}\:\mathrm{there}\:\mathrm{are}\:\mathrm{12}\:\mathrm{face}\:\mathrm{cards}\:\mathrm{the}\:\mathrm{possibility}\:\mathrm{to} \\ $$$$\mathrm{draw}\:\mathrm{one}\:\mathrm{is}\:\frac{\mathrm{12}}{\mathrm{52}}=\frac{\mathrm{3}}{\mathrm{13}} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by peter frank last updated on 05/Apr/22

$$\mathrm{what}\:\mathrm{does}\:\mathrm{it}\:\mathrm{mean}\:\mathrm{odds}\:\mathrm{in}\:\mathrm{favour}\:\mathrm{of} \\ $$$$\mathrm{getting}\:\mathrm{a}\:\mathrm{face}\:\mathrm{card}? \\ $$
Commented by peter frank last updated on 05/Apr/22
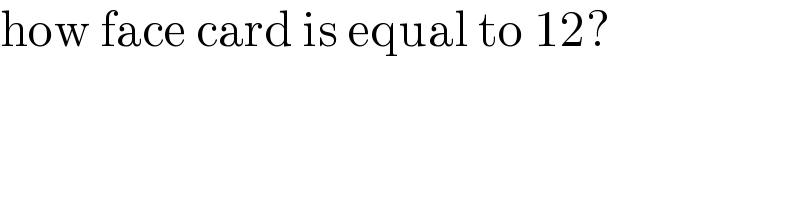
$$\mathrm{how}\:\mathrm{face}\:\mathrm{card}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{12}? \\ $$
Commented by MJS_new last updated on 06/Apr/22

$$\mathrm{a}\:\mathrm{deck}\:\mathrm{of}\:\mathrm{cards}\:\mathrm{has}\:\mathrm{4}\:\mathrm{colours} \\ $$$$\mathrm{each}\:\mathrm{colour}\:\mathrm{has}\:\mathrm{13}\:\mathrm{cards},\:\mathrm{usually} \\ $$$$\mathrm{1}\:\left(=\mathrm{ace}\right)\:\mathrm{2}\:\mathrm{3}\:\mathrm{4}\:\mathrm{5}\:\mathrm{6}\:\mathrm{7}\:\mathrm{8}\:\mathrm{9}\:\mathrm{10}\:\mathrm{knight}\:\mathrm{queen}\:\mathrm{king} \\ $$$$\left(\mathrm{or}\:\mathrm{similar}\right),\:\mathrm{where}\:\mathrm{knight}\:\mathrm{queen}\:\mathrm{king}\:\mathrm{are} \\ $$$$\mathrm{the}\:\mathrm{faces}.\:\Rightarrow\:\mathrm{3}\:\mathrm{faces}\:\mathrm{per}\:\mathrm{colour}\:\Rightarrow\:\mathrm{12}\:\mathrm{faces} \\ $$
Commented by MJS_new last updated on 06/Apr/22
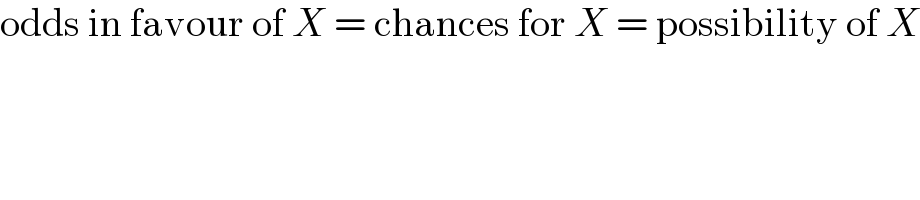
$$\mathrm{odds}\:\mathrm{in}\:\mathrm{favour}\:\mathrm{of}\:{X}\:=\:\mathrm{chances}\:\mathrm{for}\:{X}\:=\:\mathrm{possibility}\:\mathrm{of}\:{X} \\ $$
Commented by peter frank last updated on 07/Apr/22

$$\mathrm{the}\:\mathrm{ans}\:\mathrm{from}\:\mathrm{the}\:\mathrm{book}\:\mathrm{is} \\ $$$$\left(\mathrm{i}\right)\:\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{3} \\ $$
Commented by MJS_new last updated on 07/Apr/22

$$\mathrm{then}\:\mathrm{I}'\mathrm{m}\:\mathrm{sorry}.\:\mathrm{I}'\mathrm{m}\:\mathrm{no}\:\mathrm{native}\:\mathrm{English}\:\mathrm{speaker} \\ $$$$\mathrm{and}\:\mathrm{obviously}\:“\mathrm{odds}''\:\mathrm{means}\:\mathrm{something}\:\mathrm{else} \\ $$$$\mathrm{here}\:\mathrm{than}\:\mathrm{I}\:\mathrm{thought}. \\ $$
Commented by peter frank last updated on 07/Apr/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
