Question Number 168210 by mathlove last updated on 06/Apr/22
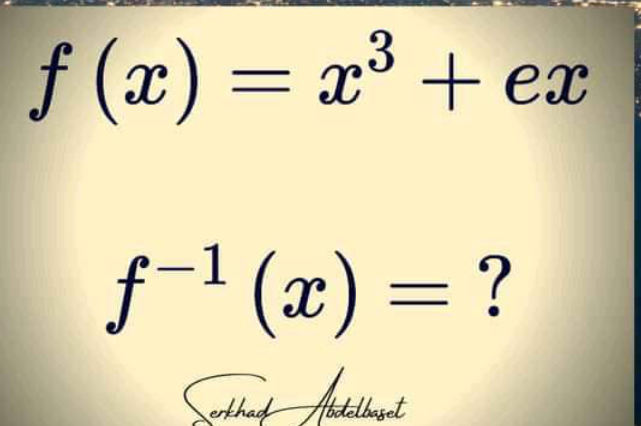
Answered by mr W last updated on 06/Apr/22
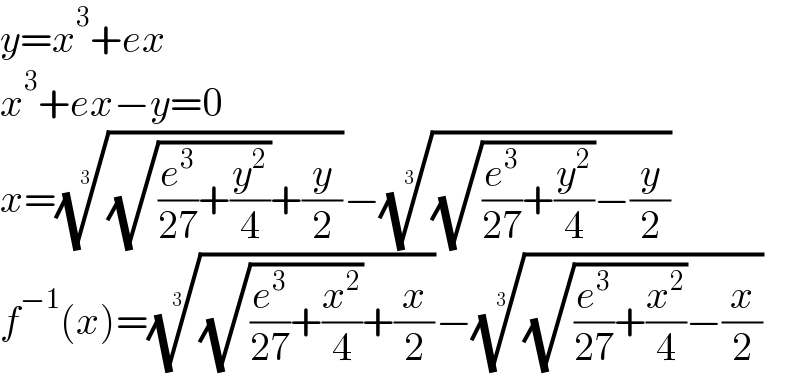
$${y}={x}^{\mathrm{3}} +{ex} \\ $$$${x}^{\mathrm{3}} +{ex}−{y}=\mathrm{0} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\sqrt{\frac{{e}^{\mathrm{3}} }{\mathrm{27}}+\frac{{y}^{\mathrm{2}} }{\mathrm{4}}}+\frac{{y}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{{e}^{\mathrm{3}} }{\mathrm{27}}+\frac{{y}^{\mathrm{2}} }{\mathrm{4}}}−\frac{{y}}{\mathrm{2}}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\sqrt[{\mathrm{3}}]{\sqrt{\frac{{e}^{\mathrm{3}} }{\mathrm{27}}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}+\frac{{x}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{{e}^{\mathrm{3}} }{\mathrm{27}}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}−\frac{{x}}{\mathrm{2}}} \\ $$
