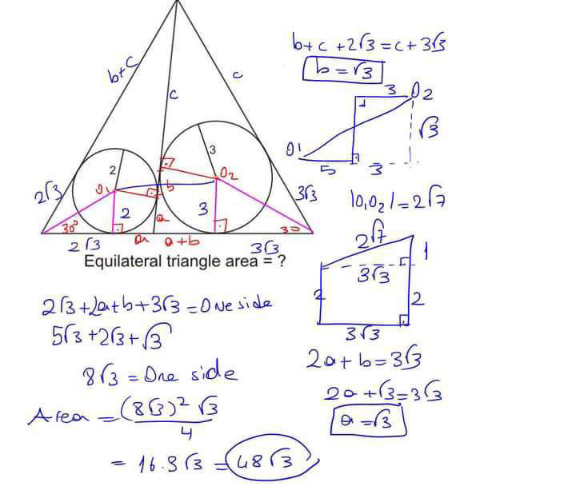
Question Number 168347 by cortano1 last updated on 08/Apr/22
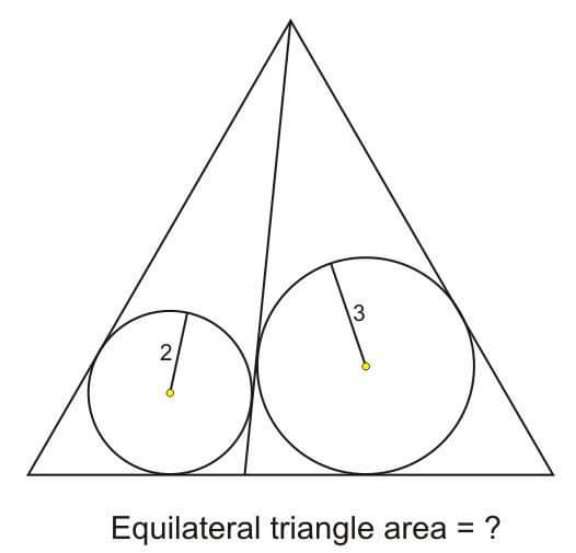
Commented by mr W last updated on 09/Apr/22
$${see}\:{Q}\mathrm{128303} \\ $$$${s}=\sqrt{\mathrm{3}}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)+\sqrt{\mathrm{3}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{8}{r}_{\mathrm{1}} {r}_{\mathrm{2}} } \\ $$$$\:\:=\sqrt{\mathrm{3}}×\mathrm{5}+\sqrt{\mathrm{3}×\mathrm{5}^{\mathrm{2}} −\mathrm{8}×\mathrm{6}}=\mathrm{8}\sqrt{\mathrm{3}} \\ $$$${A}=\frac{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{48}\sqrt{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 08/Apr/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mathman1234 last updated on 09/Apr/22
$$\mathrm{plz}\:\mathrm{help}\:\mathrm{me}\:\mathrm{and}\:\mathrm{proove}\:\mathrm{if}\:\mathrm{0}<\mathrm{a}<\mathrm{b}\:\mathrm{and}\:\mathrm{x}>\mathrm{0}\:\mathrm{that} \\ $$$$\frac{\mathrm{2}}{\pi}\left(\mathrm{1}−\frac{\mathrm{a}}{\mathrm{b}}\right)\leqslant\mathrm{sup}\mid\frac{\mathrm{sin}\left(\mathrm{ax}\right)}{\mathrm{ax}}\:−\:\frac{\mathrm{sin}\left(\mathrm{bx}\right)}{\mathrm{bx}}\mid\leqslant\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{a}}{\mathrm{b}}\right) \\ $$
Commented by mr W last updated on 09/Apr/22

$${please}\:{don}'{t}\:{put}\:{your}\:{new}\:{question}\:{in} \\ $$$${existing}\:{threads}\:{of}\:{other}\:{people}'{s} \\ $$$${questions}!\:{please}\:{open}\:{a}\:{new}\:{post} \\ $$$${for}\:{your}\:{own}\:{question}! \\ $$
Answered by infinityaction last updated on 11/Apr/22