Question Number 168366 by cortano1 last updated on 09/Apr/22
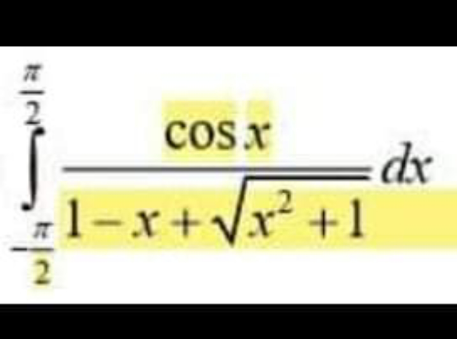
Answered by qaz last updated on 09/Apr/22
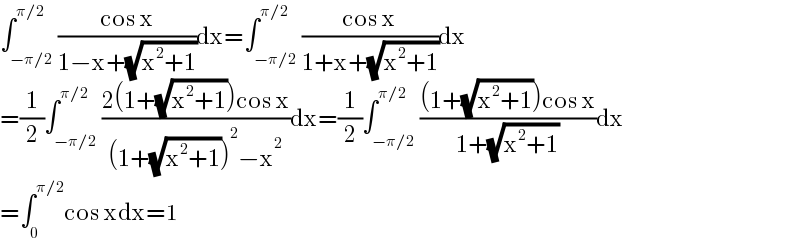
$$\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{1}−\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\mathrm{dx}=\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \frac{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{cos}\:\mathrm{x}}{\left(\mathrm{1}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \frac{\left(\mathrm{1}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:\mathrm{xdx}=\mathrm{1} \\ $$
Commented by peter frank last updated on 09/Apr/22

$$\mathrm{thanks} \\ $$
