Question Number 168459 by BegamovSirojiddin last updated on 11/Apr/22

Answered by Mathspace last updated on 11/Apr/22
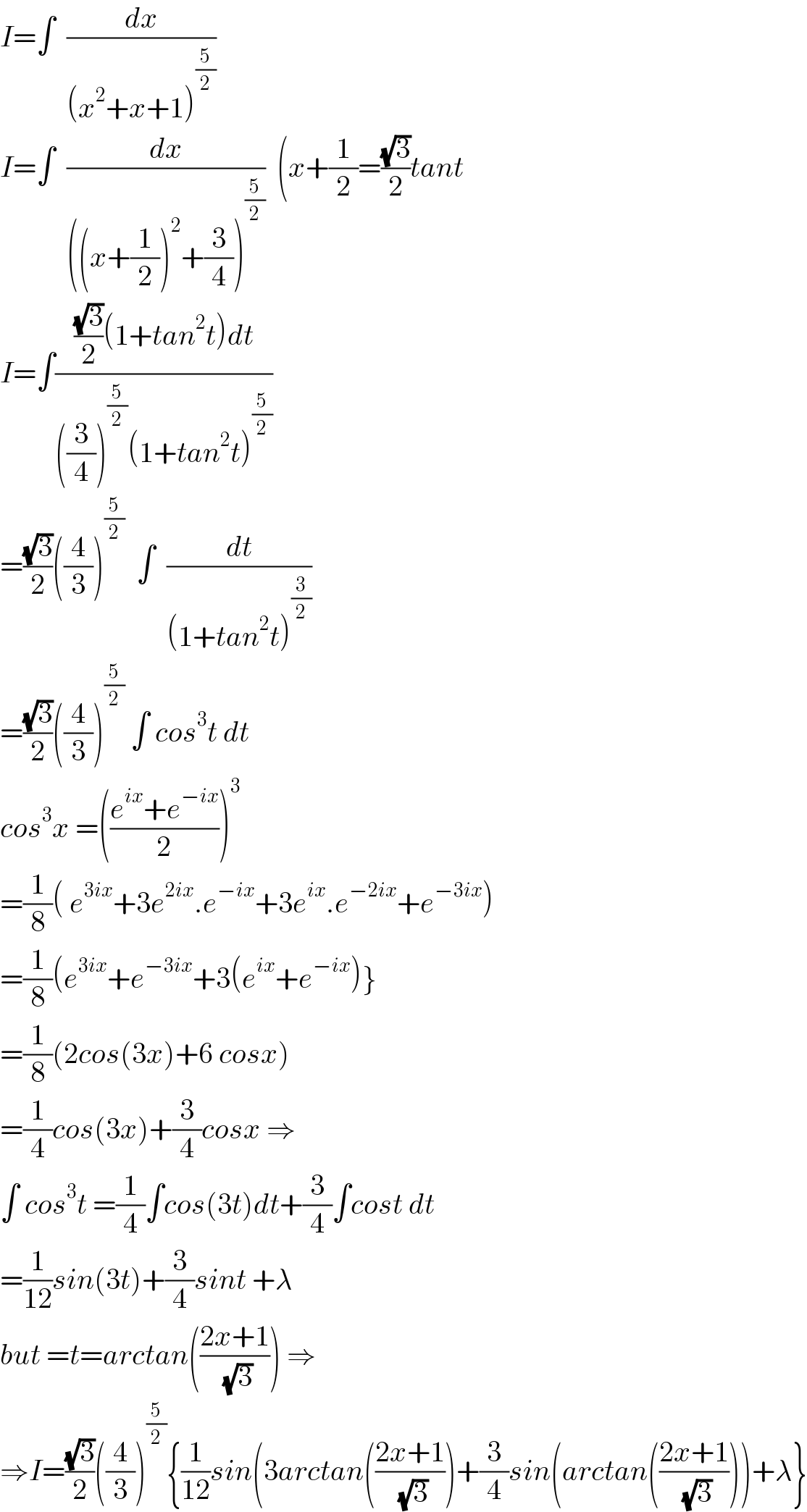
$${I}=\int\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$$${I}=\int\:\:\frac{{dx}}{\left(\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} }\:\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{tant}\right. \\ $$$${I}=\int\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt}}{\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:\:\int\:\:\frac{{dt}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:\int\:{cos}^{\mathrm{3}} {t}\:{dt} \\ $$$${cos}^{\mathrm{3}} {x}\:=\left(\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\:{e}^{\mathrm{3}{ix}} +\mathrm{3}{e}^{\mathrm{2}{ix}} .{e}^{−{ix}} +\mathrm{3}{e}^{{ix}} .{e}^{−\mathrm{2}{ix}} +{e}^{−\mathrm{3}{ix}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left({e}^{\mathrm{3}{ix}} +{e}^{−\mathrm{3}{ix}} +\mathrm{3}\left({e}^{{ix}} +{e}^{−{ix}} \right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{2}{cos}\left(\mathrm{3}{x}\right)+\mathrm{6}\:{cosx}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{3}{x}\right)+\frac{\mathrm{3}}{\mathrm{4}}{cosx}\:\Rightarrow \\ $$$$\int\:{cos}^{\mathrm{3}} {t}\:=\frac{\mathrm{1}}{\mathrm{4}}\int{cos}\left(\mathrm{3}{t}\right){dt}+\frac{\mathrm{3}}{\mathrm{4}}\int{cost}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}{sin}\left(\mathrm{3}{t}\right)+\frac{\mathrm{3}}{\mathrm{4}}{sint}\:+\lambda \\ $$$${but}\:={t}={arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\Rightarrow{I}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \left\{\frac{\mathrm{1}}{\mathrm{12}}{sin}\left(\mathrm{3}{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{3}}{\mathrm{4}}{sin}\left({arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)+\lambda\right\}\right. \\ $$
Answered by MJS_new last updated on 11/Apr/22
![∫(dx/((x^2 +x+1)^(5/2) ))= [t=((2x+1+2(√(x^2 +x+1)))/( (√3))) → dx=((√(x^2 +x+1))/t)dt] =((256)/9)∫(t^3 /((t^2 +1)^4 ))dt=((256)/9)∫((t/((t^2 +1)^3 ))−(t/((t^2 +1)^4 )))dt= =−((64)/(9(t^2 +1)^2 ))+((128)/(27(t^2 +1)^3 ))=−((64(3t^2 +1))/(27(t^2 +1)^3 ))= =((2(2x+1)(8x^2 +8x+11))/(27(x^2 +x+1)^(3/2) ))+C](https://www.tinkutara.com/question/Q168483.png)
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{5}/\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{t}}{dt}\right] \\ $$$$=\frac{\mathrm{256}}{\mathrm{9}}\int\frac{{t}^{\mathrm{3}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }{dt}=\frac{\mathrm{256}}{\mathrm{9}}\int\left(\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }−\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }\right){dt}= \\ $$$$=−\frac{\mathrm{64}}{\mathrm{9}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{128}}{\mathrm{27}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=−\frac{\mathrm{64}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{27}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$=\frac{\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{11}\right)}{\mathrm{27}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }+{C} \\ $$
