Question Number 168489 by infinityaction last updated on 11/Apr/22
Commented by infinityaction last updated on 11/Apr/22

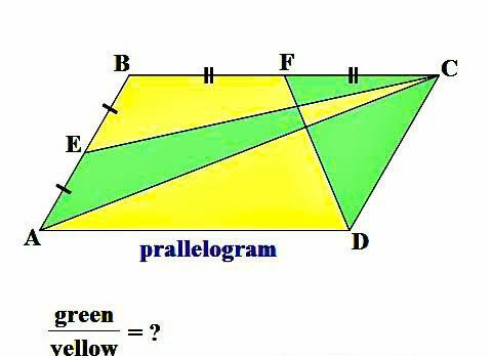
$${please}\:{solve}\:{this}\:{problem} \\ $$
Answered by mr W last updated on 12/Apr/22

Commented by mr W last updated on 12/Apr/22
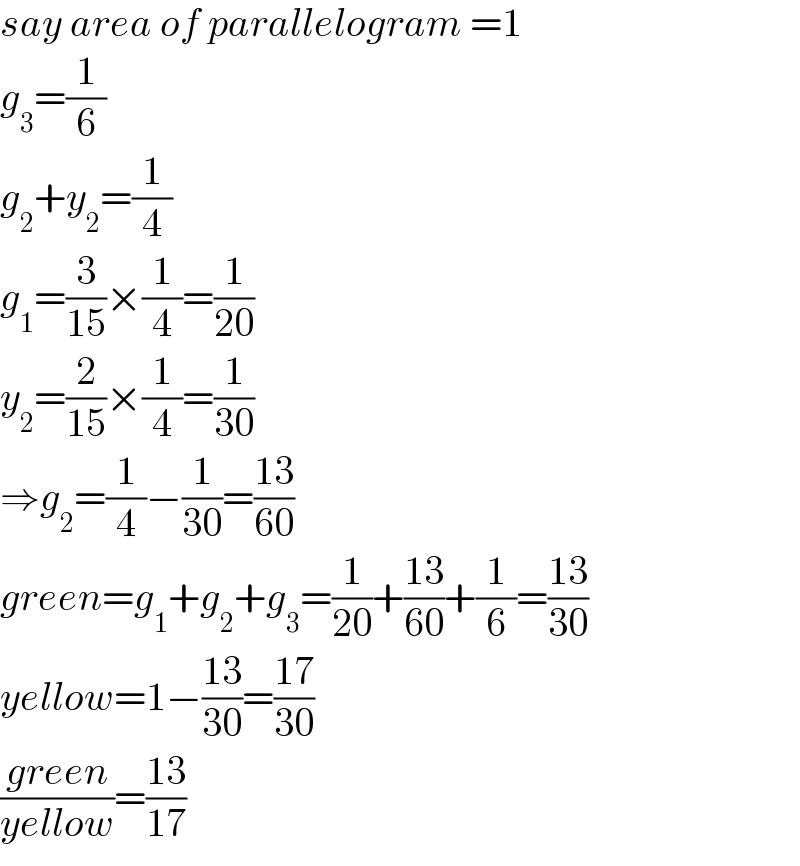
$${say}\:{area}\:{of}\:{parallelogram}\:=\mathrm{1} \\ $$$${g}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${g}_{\mathrm{2}} +{y}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${g}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{15}}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{20}} \\ $$$${y}_{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{15}}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{30}} \\ $$$$\Rightarrow{g}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{30}}=\frac{\mathrm{13}}{\mathrm{60}} \\ $$$${green}={g}_{\mathrm{1}} +{g}_{\mathrm{2}} +{g}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{13}}{\mathrm{60}}+\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{13}}{\mathrm{30}} \\ $$$${yellow}=\mathrm{1}−\frac{\mathrm{13}}{\mathrm{30}}=\frac{\mathrm{17}}{\mathrm{30}} \\ $$$$\frac{{green}}{{yellow}}=\frac{\mathrm{13}}{\mathrm{17}} \\ $$
Commented by Tawa11 last updated on 12/Apr/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by Ari last updated on 12/Apr/22

Commented by Ari last updated on 12/Apr/22
can you speak please?
Commented by mr W last updated on 12/Apr/22
Commented by mr W last updated on 12/Apr/22
![((HC)/(AH))=((FH)/(HD))=((FC)/(AD))=(1/2) ⇒((HC)/(AC))=(1/3) ⇒((FH)/(FD))=(1/3) ((EF)/(AC))=(1/2) ((FG)/(GH))=((EF)/(HC))=((AC/2)/(AC/3))=(3/2) ((FG)/(FH))=(3/(2+3))=(3/5) ((FG)/(FD))=((3/5∗FH)/(FD))=((3/5∗1/3∗FD)/(FD))=(1/5) ((GH)/(FD))=((2/5∗FH)/(FD))=((2/5∗1/3∗FD)/(FD))=(2/(15)) ((HD)/(FD))=(2/3) [FCD]=((parallelogram)/4)=(1/4) g_1 =(1/5)×[FCD]=(1/5)×(1/4)=(1/(20)) g_3 =(2/3)×[FCD]=(2/3)×(1/4)=(1/6) y_2 =(2/(15))×[FCD]=(2/(15))×(1/4)=(1/(30)) g_2 +y_2 =((parallelogram)/4)=(1/4) ⇒g_2 =(1/4)−(1/(30))=((13)/(60)) g_1 +g_2 +g_3 =(1/(20))+((13)/(60))+(1/6)=((13)/(30))](https://www.tinkutara.com/question/Q168535.png)
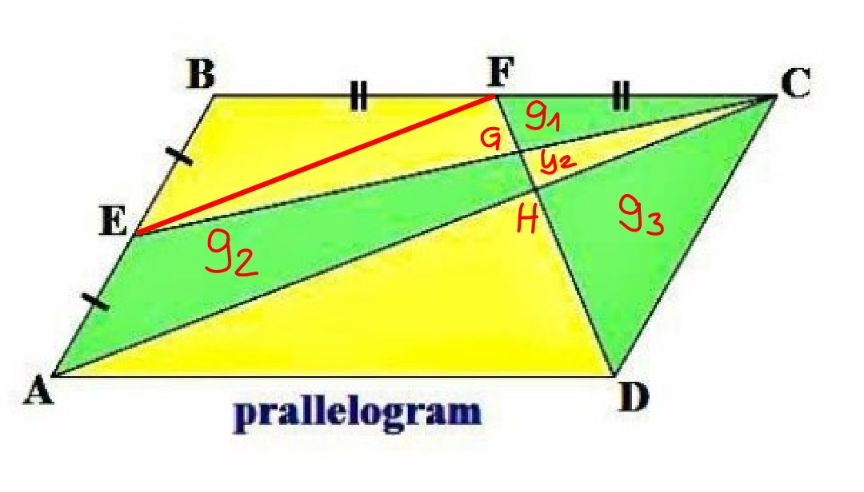
$$\frac{{HC}}{{AH}}=\frac{{FH}}{{HD}}=\frac{{FC}}{{AD}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{HC}}{{AC}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{FH}}{{FD}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{{EF}}{{AC}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{FG}}{{GH}}=\frac{{EF}}{{HC}}=\frac{{AC}/\mathrm{2}}{{AC}/\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\frac{{FG}}{{FH}}=\frac{\mathrm{3}}{\mathrm{2}+\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{{FG}}{{FD}}=\frac{\mathrm{3}/\mathrm{5}\ast{FH}}{{FD}}=\frac{\mathrm{3}/\mathrm{5}\ast\mathrm{1}/\mathrm{3}\ast{FD}}{{FD}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\frac{{GH}}{{FD}}=\frac{\mathrm{2}/\mathrm{5}\ast{FH}}{{FD}}=\frac{\mathrm{2}/\mathrm{5}\ast\mathrm{1}/\mathrm{3}\ast{FD}}{{FD}}=\frac{\mathrm{2}}{\mathrm{15}} \\ $$$$\frac{{HD}}{{FD}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\left[{FCD}\right]=\frac{{parallelogram}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${g}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{5}}×\left[{FCD}\right]=\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{20}} \\ $$$${g}_{\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{3}}×\left[{FCD}\right]=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${y}_{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{15}}×\left[{FCD}\right]=\frac{\mathrm{2}}{\mathrm{15}}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{30}} \\ $$$${g}_{\mathrm{2}} +{y}_{\mathrm{2}} =\frac{{parallelogram}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{g}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{30}}=\frac{\mathrm{13}}{\mathrm{60}} \\ $$$${g}_{\mathrm{1}} +{g}_{\mathrm{2}} +{g}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{13}}{\mathrm{60}}+\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{13}}{\mathrm{30}} \\ $$
Commented by Ari last updated on 12/Apr/22
thanks Mr.W!
