Question Number 168493 by mokys last updated on 11/Apr/22

Answered by FelipeLz last updated on 12/Apr/22
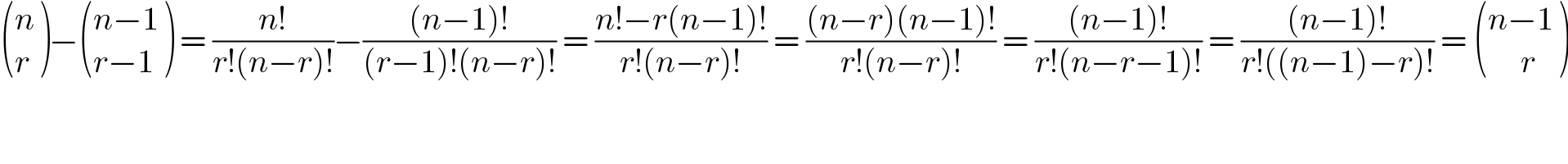
$$\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}−\begin{pmatrix}{{n}−\mathrm{1}}\\{{r}−\mathrm{1}}\end{pmatrix}\:=\:\frac{{n}!}{{r}!\left({n}−{r}\right)!}−\frac{\left({n}−\mathrm{1}\right)!}{\left({r}−\mathrm{1}\right)!\left({n}−{r}\right)!}\:=\:\frac{{n}!−{r}\left({n}−\mathrm{1}\right)!}{{r}!\left({n}−{r}\right)!}\:=\:\frac{\left({n}−{r}\right)\left({n}−\mathrm{1}\right)!}{{r}!\left({n}−{r}\right)!}\:=\:\frac{\left({n}−\mathrm{1}\right)!}{{r}!\left({n}−{r}−\mathrm{1}\right)!}\:=\:\frac{\left({n}−\mathrm{1}\right)!}{{r}!\left(\left({n}−\mathrm{1}\right)−{r}\right)!}\:=\:\begin{pmatrix}{{n}−\mathrm{1}}\\{\:\:\:\:\:{r}}\end{pmatrix} \\ $$
