Question Number 168499 by infinityaction last updated on 12/Apr/22

Answered by MJS_new last updated on 12/Apr/22
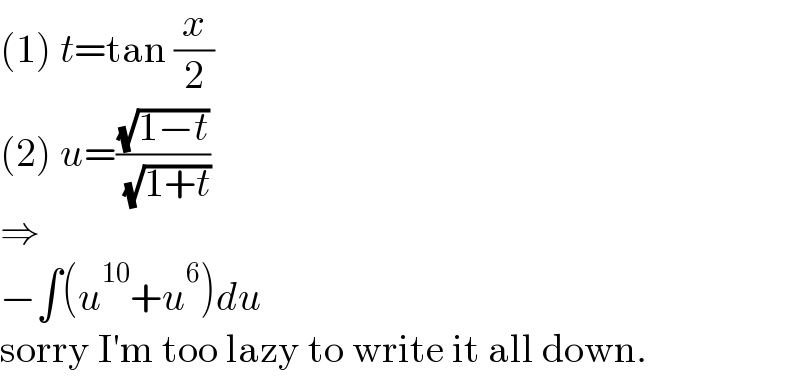
$$\left(\mathrm{1}\right)\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:{u}=\frac{\sqrt{\mathrm{1}−{t}}}{\:\sqrt{\mathrm{1}+{t}}} \\ $$$$\Rightarrow \\ $$$$−\int\left({u}^{\mathrm{10}} +{u}^{\mathrm{6}} \right){du} \\ $$$$\mathrm{sorry}\:\mathrm{I}'\mathrm{m}\:\mathrm{too}\:\mathrm{lazy}\:\mathrm{to}\:\mathrm{write}\:\mathrm{it}\:\mathrm{all}\:\mathrm{down}. \\ $$
Commented by infinityaction last updated on 12/Apr/22
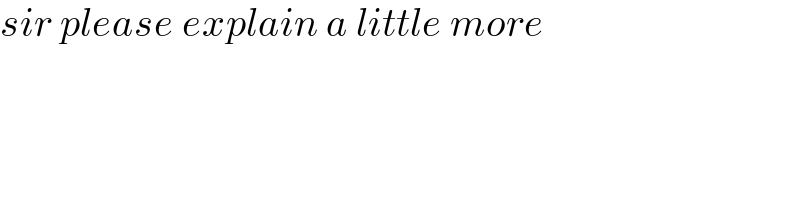
$${sir}\:{please}\:{explain}\:{a}\:{little}\:{more} \\ $$
Answered by MJS_new last updated on 12/Apr/22
![easier: ∫((sec^2 x)/((sec x +tan x)^(9/2) ))dx= [t=sin x → dx=(dt/(cos x))] =∫(((1−t)^(3/4) )/((1+t)^(15/4) ))dt= [u=(((1−t)^(1/4) )/((1+t)^(1/4) )) → dt=−2(1−t)^(3/4) (1+t)^(5/4) du] =−∫u^(10) +u^6 du=−(u^(11) /(11))−(u^7 /7)= =−((2(9+2t)(1−t)^(7/4) )/(77(1+t)^(11/4) ))= =−((2(9+2sin x)(1−sin x)^(7/4) )/(77(1+sin x)^(11/4) ))+C](https://www.tinkutara.com/question/Q168547.png)
$$\mathrm{easier}: \\ $$$$\int\frac{\mathrm{sec}^{\mathrm{2}} \:{x}}{\left(\mathrm{sec}\:{x}\:+\mathrm{tan}\:{x}\right)^{\mathrm{9}/\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{cos}\:{x}}\right] \\ $$$$=\int\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{3}/\mathrm{4}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{15}/\mathrm{4}} }{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{1}/\mathrm{4}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{1}/\mathrm{4}} }\:\rightarrow\:{dt}=−\mathrm{2}\left(\mathrm{1}−{t}\right)^{\mathrm{3}/\mathrm{4}} \left(\mathrm{1}+{t}\right)^{\mathrm{5}/\mathrm{4}} {du}\right] \\ $$$$=−\int{u}^{\mathrm{10}} +{u}^{\mathrm{6}} {du}=−\frac{{u}^{\mathrm{11}} }{\mathrm{11}}−\frac{{u}^{\mathrm{7}} }{\mathrm{7}}= \\ $$$$=−\frac{\mathrm{2}\left(\mathrm{9}+\mathrm{2}{t}\right)\left(\mathrm{1}−{t}\right)^{\mathrm{7}/\mathrm{4}} }{\mathrm{77}\left(\mathrm{1}+{t}\right)^{\mathrm{11}/\mathrm{4}} }= \\ $$$$=−\frac{\mathrm{2}\left(\mathrm{9}+\mathrm{2sin}\:{x}\right)\left(\mathrm{1}−\mathrm{sin}\:{x}\right)^{\mathrm{7}/\mathrm{4}} }{\mathrm{77}\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{11}/\mathrm{4}} }+{C} \\ $$
Commented by peter frank last updated on 13/Apr/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by infinityaction last updated on 13/Apr/22

$${thank}\:{you}\:{sir} \\ $$
