Question-168558

Question Number 168558 by ajfour last updated on 13/Apr/22

Commented by ajfour last updated on 13/Apr/22

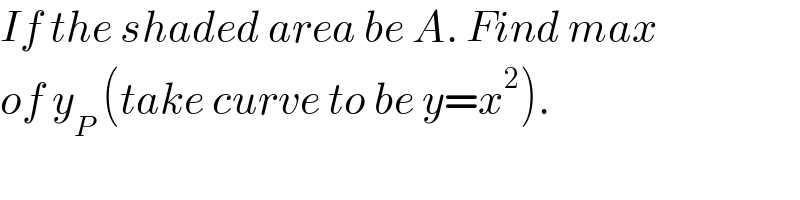
If the shaded area be A. Find max of y_P (take curve to be y=x^2 ).

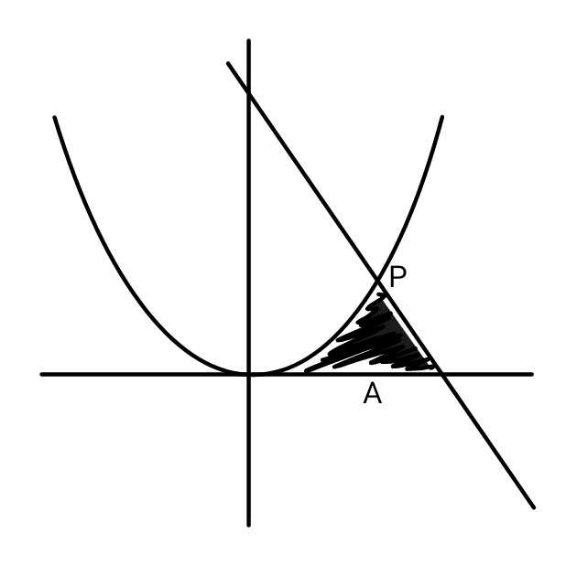
$${If}\:{the}\:{shaded}\:{area}\:{be}\:{A}.\:{Find}\:{max} \\ $$$${of}\:{y}_{{P}} \:\left({take}\:{curve}\:{to}\:{be}\:{y}={x}^{\mathrm{2}} \right). \\ $$

Answered by mr W last updated on 13/Apr/22

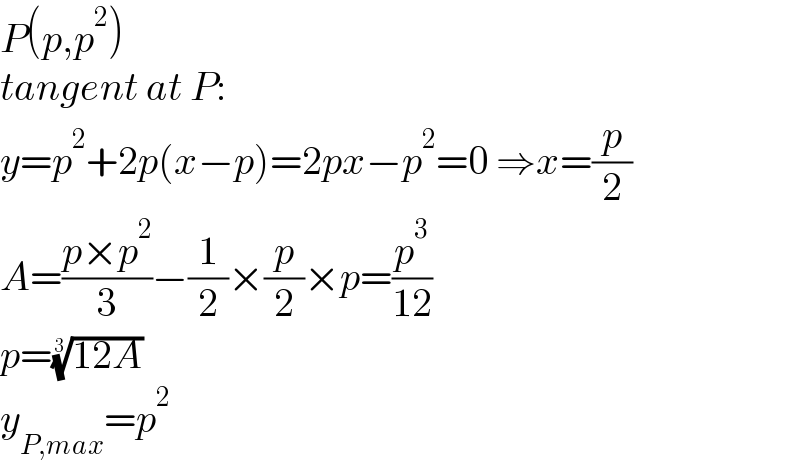
P(p,p^2 ) tangent at P: y=p^2 +2p(x−p)=2px−p^2 =0 ⇒x=(p/2) A=((p×p^2 )/3)−(1/2)×(p/2)×p=(p^3 /(12)) p=((12A))^(1/3) y_(P,max) =p^2

$${P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${tangent}\:{at}\:{P}: \\ $$$${y}={p}^{\mathrm{2}} +\mathrm{2}{p}\left({x}−{p}\right)=\mathrm{2}{px}−{p}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow{x}=\frac{{p}}{\mathrm{2}} \\ $$$${A}=\frac{{p}×{p}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{{p}}{\mathrm{2}}×{p}=\frac{{p}^{\mathrm{3}} }{\mathrm{12}} \\ $$$${p}=\sqrt[{\mathrm{3}}]{\mathrm{12}{A}} \\ $$$${y}_{{P},{max}} ={p}^{\mathrm{2}} \\ $$

Commented by Tawa11 last updated on 13/Apr/22

$$\mathrm{Nice}\:\mathrm{sir}. \\ $$

Commented by ajfour last updated on 16/Apr/22

$${Thank}\:{u}\:{sir}. \\ $$

Commented by mr W last updated on 13/Apr/22

Commented by mr W last updated on 13/Apr/22

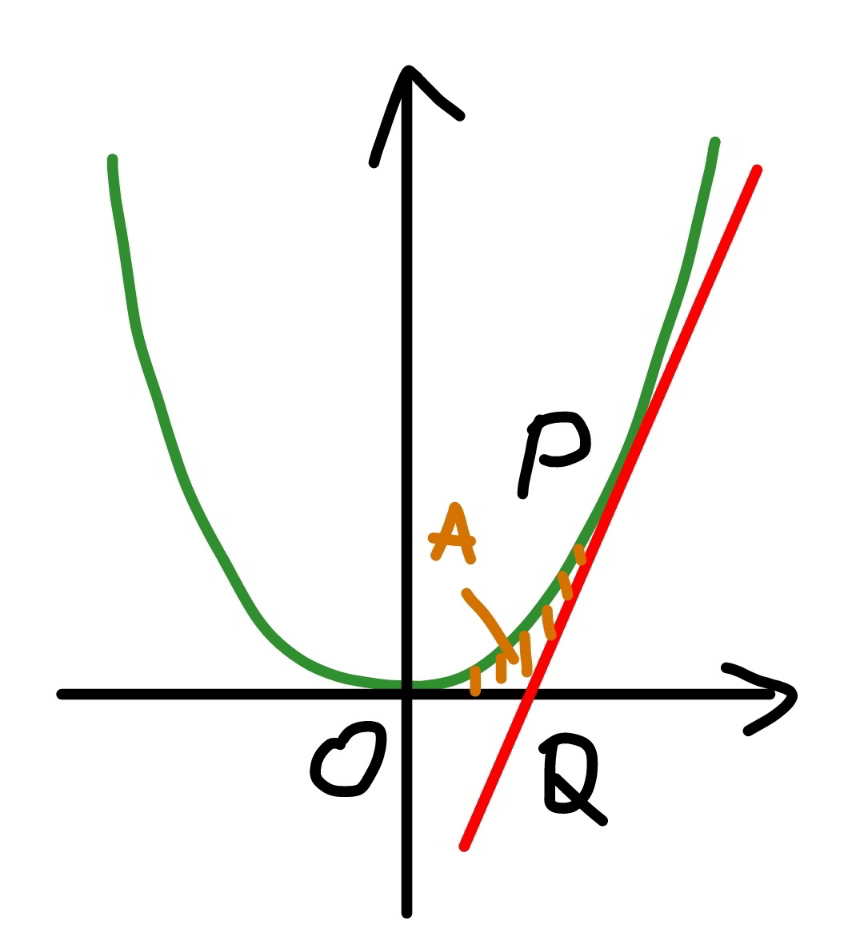
$${when}\:{P}\:{is}\:{given},\:{area}\:{of}\:{OPQ}\:{A}\:{is}\: \\ $$$${minimum},\:{when}\:{PQ}\:{is}\:{tangent}. \\ $$$${similarly}\:{when}\:{area}\:{A}\:{is}\:{given},\:{P} \\ $$$${is}\:{highest}\:{when}\:{PQ}\:{is}\:{tangent}. \\ $$

Answered by mindispower last updated on 13/Apr/22

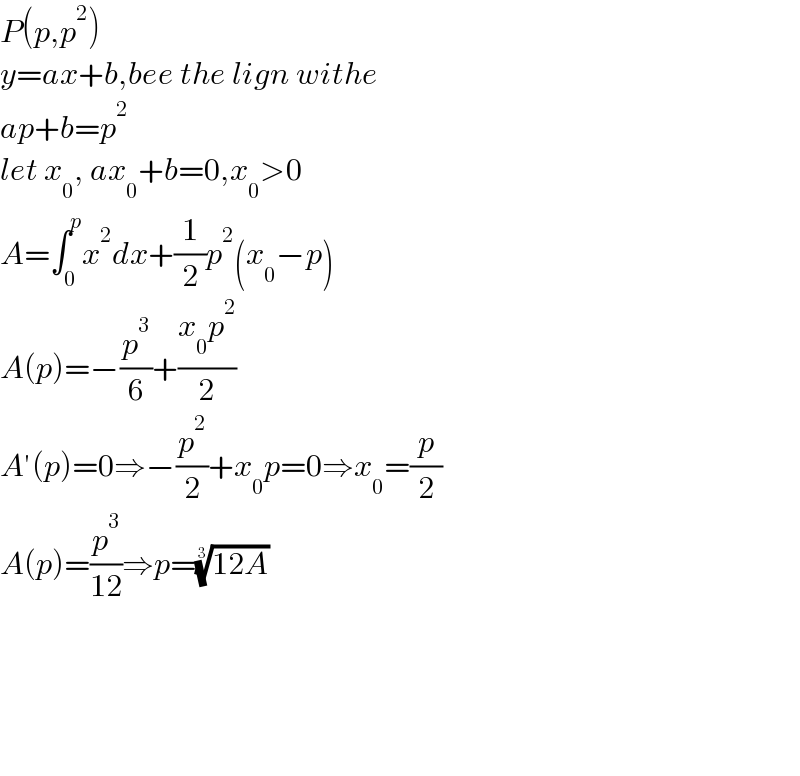
P(p,p^2 ) y=ax+b,bee the lign withe ap+b=p^2 let x_0 , ax_0 +b=0,x_0 >0 A=∫_0 ^p x^2 dx+(1/2)p^2 (x_0 −p) A(p)=−(p^3 /6)+((x_0 p^2 )/2) A′(p)=0⇒−(p^2 /2)+x_0 p=0⇒x_0 =(p/2) A(p)=(p^3 /(12))⇒p=((12A))^(1/3)

$${P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${y}={ax}+{b},{bee}\:{the}\:{lign}\:{withe} \\ $$$${ap}+{b}={p}^{\mathrm{2}} \\ $$$${let}\:{x}_{\mathrm{0}} ,\:{ax}_{\mathrm{0}} +{b}=\mathrm{0},{x}_{\mathrm{0}} >\mathrm{0} \\ $$$${A}=\int_{\mathrm{0}} ^{{p}} {x}^{\mathrm{2}} {dx}+\frac{\mathrm{1}}{\mathrm{2}}{p}^{\mathrm{2}} \left({x}_{\mathrm{0}} −{p}\right) \\ $$$${A}\left({p}\right)=−\frac{{p}^{\mathrm{3}} }{\mathrm{6}}+\frac{{x}_{\mathrm{0}} {p}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${A}'\left({p}\right)=\mathrm{0}\Rightarrow−\frac{{p}^{\mathrm{2}} }{\mathrm{2}}+{x}_{\mathrm{0}} {p}=\mathrm{0}\Rightarrow{x}_{\mathrm{0}} =\frac{{p}}{\mathrm{2}} \\ $$$${A}\left({p}\right)=\frac{{p}^{\mathrm{3}} }{\mathrm{12}}\Rightarrow{p}=\sqrt[{\mathrm{3}}]{\mathrm{12}{A}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by ajfour last updated on 16/Apr/22

$${Thank}\:{you}\:{sir}. \\ $$

Commented by mindispower last updated on 19/Apr/22

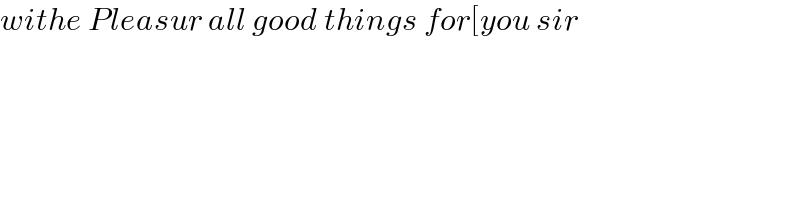
withe Pleasur all good things for[you sir

$${withe}\:{Pleasur}\:{all}\:{good}\:{things}\:{for}\left[{you}\:{sir}\right. \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply