Question-168721

Question Number 168721 by mathlove last updated on 16/Apr/22

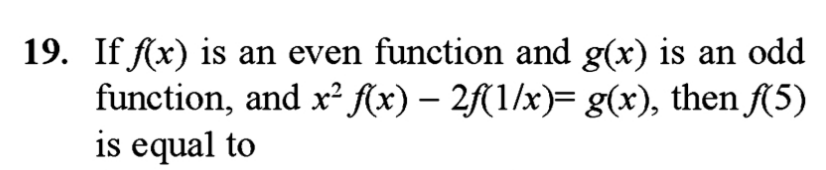
Answered by Rasheed.Sindhi last updated on 16/Apr/22

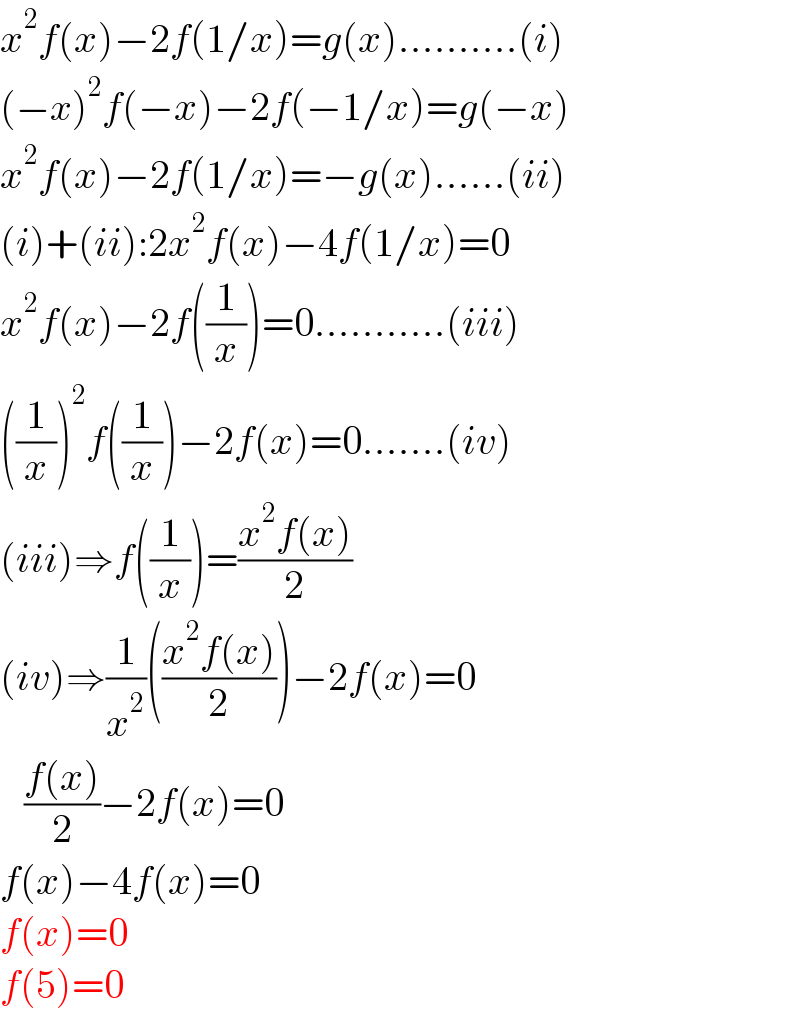
x^2 f(x)−2f(1/x)=g(x)..........(i) (−x)^2 f(−x)−2f(−1/x)=g(−x) x^2 f(x)−2f(1/x)=−g(x)......(ii) (i)+(ii):2x^2 f(x)−4f(1/x)=0 x^2 f(x)−2f((1/x))=0...........(iii) ((1/x))^2 f((1/x))−2f(x)=0.......(iv) (iii)⇒f((1/x))=((x^2 f(x))/2) (iv)⇒(1/x^2 )(((x^2 f(x))/2))−2f(x)=0 ((f(x))/2)−2f(x)=0 f(x)−4f(x)=0 f(x)=0 f(5)=0

$${x}^{\mathrm{2}} {f}\left({x}\right)−\mathrm{2}{f}\left(\mathrm{1}/{x}\right)={g}\left({x}\right)……….\left({i}\right) \\ $$$$\left(−{x}\right)^{\mathrm{2}} {f}\left(−{x}\right)−\mathrm{2}{f}\left(−\mathrm{1}/{x}\right)={g}\left(−{x}\right) \\ $$$${x}^{\mathrm{2}} {f}\left({x}\right)−\mathrm{2}{f}\left(\mathrm{1}/{x}\right)=−{g}\left({x}\right)……\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right):\mathrm{2}{x}^{\mathrm{2}} {f}\left({x}\right)−\mathrm{4}{f}\left(\mathrm{1}/{x}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} {f}\left({x}\right)−\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{0}………..\left({iii}\right) \\ $$$$\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} {f}\left(\frac{\mathrm{1}}{{x}}\right)−\mathrm{2}{f}\left({x}\right)=\mathrm{0}…….\left({iv}\right) \\ $$$$\left({iii}\right)\Rightarrow{f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{{x}^{\mathrm{2}} {f}\left({x}\right)}{\mathrm{2}} \\ $$$$\left({iv}\right)\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\frac{{x}^{\mathrm{2}} {f}\left({x}\right)}{\mathrm{2}}\right)−\mathrm{2}{f}\left({x}\right)=\mathrm{0} \\ $$$$\:\:\:\frac{{f}\left({x}\right)}{\mathrm{2}}−\mathrm{2}{f}\left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)−\mathrm{4}{f}\left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{5}\right)=\mathrm{0} \\ $$

Commented by mathlove last updated on 16/Apr/22

$${thanks}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply