Menu Close

Question-168732

Tinku Tara 0 Comments
Pin




Question Number 168732 by mnjuly1970 last updated on 16/Apr/22
Answered by mnjuly1970 last updated on 16/Apr/22
Ω = ∫_0 ^( ∞) (( x^( (1/4)) + 2x^( (5/4)) +x^( (9/4)) )/((1+x^( 3) )^( 2) ))dx =^(x^( 3) = t) (1/3)∫_0 ^( ∞) ((t^( (1/(12))−(8/(12))) + 2t^( (5/(12))−(8/(12))) + t^( (9/(12))−(8/(12))) )/((1 + t )^( 2) )) dt = (1/3) ∫_0 ^( ∞) ((t^( ((−7)/(12))) +2t^( ((−1)/4)) + t^( ((−1)/(12))) )/((1+ t )^( 2) ))dt = (1/(3 )) ∫_0 ^( ∞) ((t^( (5/(12)) −1) + 2t^( (3/4) −1) + t^( ((11)/(12))−1) )/((1 + t )^( 2) ))dt = (1/3) { β ((5/(12)) , ((19)/(12))) +2β((3/4) , (5/4)) +β (((11)/(12)) , ((13)/(12)) } = (1/3) { ((Γ((5/(12)) )Γ( ((19)/(12)))+2Γ((3/4))Γ((5/4))+Γ (((11)/(12)))Γ (((13)/(12)) ) )/([Γ(2)= 1 ]))} = (1/3) { (7/(12)) (π/(sin(((5π)/(12))))) +(1/2) (π/(sin((π/4)))) +(1/(12)) (π/(sin((π/(12))))) } = (1/3) { (7/(3 )) (π/( (√6) +(√2))) + (π/( (√2))) +(1/3) (π/( (√6) −(√2))) } = (π/3) { ((7((√6) −(√2) ))/(12)) +(1/( (√2))) + (((√6) +(√2))/(12)) } = (π/3) { ((8(√6) −6(√2) )/(12)) + (1/( (√2) )) } = (π/3)(((8(√6))/(12)))= (2/3) ((√6)/3)π = (2/3)(√(2/3)) π ∴ Ω = (√(4/9)) ((((4/9))))^(1/4) π a − 1 = (4/9) ⇒ a = ((13)/9) ✓
$$\:\:\:\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{x}^{\:\frac{\mathrm{1}}{\mathrm{4}}} +\:\mathrm{2}{x}^{\:\:\frac{\mathrm{5}}{\mathrm{4}}} +{x}^{\:\frac{\mathrm{9}}{\mathrm{4}}} }{\left(\mathrm{1}+{x}^{\:\mathrm{3}} \right)^{\:\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\overset{{x}^{\:\mathrm{3}} =\:{t}} {=}\:\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\:\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{8}}{\mathrm{12}}} \:+\:\mathrm{2}{t}^{\:\frac{\mathrm{5}}{\mathrm{12}}−\frac{\mathrm{8}}{\mathrm{12}}} +\:{t}^{\:\frac{\mathrm{9}}{\mathrm{12}}−\frac{\mathrm{8}}{\mathrm{12}}} }{\left(\mathrm{1}\:+\:{t}\:\right)^{\:\mathrm{2}} }\:{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\:\frac{−\mathrm{7}}{\mathrm{12}}} +\mathrm{2}{t}^{\:\frac{−\mathrm{1}}{\mathrm{4}}} +\:{t}^{\:\frac{−\mathrm{1}}{\mathrm{12}}} \:}{\left(\mathrm{1}+\:{t}\:\right)^{\:\mathrm{2}} }{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}\:}\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{t}^{\:\frac{\mathrm{5}}{\mathrm{12}}\:−\mathrm{1}} +\:\mathrm{2}{t}^{\:\frac{\mathrm{3}}{\mathrm{4}}\:−\mathrm{1}} +\:{t}^{\:\frac{\mathrm{11}}{\mathrm{12}}−\mathrm{1}} }{\left(\mathrm{1}\:+\:{t}\:\right)^{\:\mathrm{2}} }{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left\{\:\beta\:\left(\frac{\mathrm{5}}{\mathrm{12}}\:,\:\frac{\mathrm{19}}{\mathrm{12}}\right)\:+\mathrm{2}\beta\left(\frac{\mathrm{3}}{\mathrm{4}}\:,\:\frac{\mathrm{5}}{\mathrm{4}}\right)\:+\beta\:\left(\frac{\mathrm{11}}{\mathrm{12}}\:,\:\frac{\mathrm{13}}{\mathrm{12}}\:\right\}\right. \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left\{\:\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{12}}\:\right)\Gamma\left(\:\frac{\mathrm{19}}{\mathrm{12}}\right)+\mathrm{2}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right)+\Gamma\:\left(\frac{\mathrm{11}}{\mathrm{12}}\right)\Gamma\:\left(\frac{\mathrm{13}}{\mathrm{12}}\:\right)\:}{\left[\Gamma\left(\mathrm{2}\right)=\:\mathrm{1}\:\right]}\right\} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left\{\:\frac{\mathrm{7}}{\mathrm{12}}\:\frac{\pi}{{sin}\left(\frac{\mathrm{5}\pi}{\mathrm{12}}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:+\frac{\mathrm{1}}{\mathrm{12}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{12}}\right)}\:\right\} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left\{\:\frac{\mathrm{7}}{\mathrm{3}\:}\:\frac{\pi}{\:\sqrt{\mathrm{6}}\:+\sqrt{\mathrm{2}}}\:+\:\frac{\pi}{\:\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:\frac{\pi}{\:\sqrt{\mathrm{6}}\:−\sqrt{\mathrm{2}}}\:\right\} \\ $$$$\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{3}}\:\left\{\:\frac{\mathrm{7}\left(\sqrt{\mathrm{6}}\:−\sqrt{\mathrm{2}}\:\right)}{\mathrm{12}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\:\frac{\sqrt{\mathrm{6}}\:+\sqrt{\mathrm{2}}}{\mathrm{12}}\:\right\} \\ $$$$\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{3}}\:\left\{\:\frac{\mathrm{8}\sqrt{\mathrm{6}}\:−\mathrm{6}\sqrt{\mathrm{2}}\:}{\mathrm{12}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\:\right\} \\ $$$$\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{3}}\left(\frac{\mathrm{8}\sqrt{\mathrm{6}}}{\mathrm{12}}\right)=\:\frac{\mathrm{2}}{\mathrm{3}}\:\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\pi\:=\:\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\:\pi \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\Omega\:=\:\sqrt{\frac{\mathrm{4}}{\mathrm{9}}}\:\sqrt[{\mathrm{4}}]{\left(\frac{\mathrm{4}}{\mathrm{9}}\right)}\:\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\:−\:\mathrm{1}\:=\:\frac{\mathrm{4}}{\mathrm{9}}\:\Rightarrow\:{a}\:=\:\frac{\mathrm{13}}{\mathrm{9}}\:\:\:\:\:\:\:\checkmark \\ $$$$\:\: \\ $$
Commented by safojontoshtemirov last updated on 16/Apr/22
very nice ��
Commented by Tawa11 last updated on 16/Apr/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by Mathspace last updated on 17/Apr/22
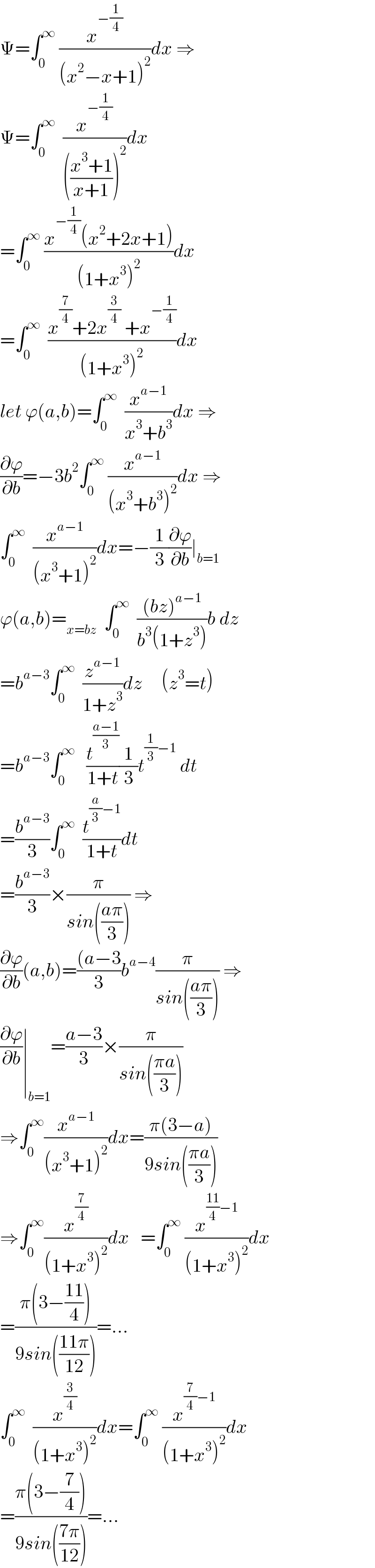
Ψ=∫_0 ^∞ (x^(−(1/4)) /((x^2 −x+1)^2 ))dx ⇒ Ψ=∫_0 ^∞ (x^(−(1/4)) /((((x^3 +1)/(x+1)))^2 ))dx =∫_0 ^∞ ((x^(−(1/4)) (x^2 +2x+1))/((1+x^3 )^2 ))dx =∫_0 ^∞ ((x^(7/4) +2x^(3/4) +x^(−(1/4)) )/((1+x^3 )^2 ))dx let ϕ(a,b)=∫_0 ^∞ (x^(a−1) /(x^3 +b^3 ))dx ⇒ (∂ϕ/∂b)=−3b^2 ∫_0 ^∞ (x^(a−1) /((x^3 +b^3 )^2 ))dx ⇒ ∫_0 ^∞ (x^(a−1) /((x^3 +1)^2 ))dx=−(1/3)(∂ϕ/∂b)∣_(b=1) ϕ(a,b)=_(x=bz) ∫_0 ^∞ (((bz)^(a−1) )/(b^3 (1+z^3 )))b dz =b^(a−3) ∫_0 ^∞ (z^(a−1) /(1+z^3 ))dz (z^3 =t) =b^(a−3) ∫_0 ^∞ (t^((a−1)/3) /(1+t))(1/3)t^((1/3)−1) dt =(b^(a−3) /3)∫_0 ^∞ (t^((a/3)−1) /(1+t))dt =(b^(a−3) /3)×(π/(sin(((aπ)/3)))) ⇒ (∂ϕ/∂b)(a,b)=(((a−3)/3)b^(a−4) (π/(sin(((aπ)/3)))) ⇒ (∂ϕ/∂b)∣_(b=1) =((a−3)/3)×(π/(sin(((πa)/3)))) ⇒∫_0 ^∞ (x^(a−1) /((x^3 +1)^2 ))dx=((π(3−a))/(9sin(((πa)/3)))) ⇒∫_0 ^∞ (x^(7/4) /((1+x^3 )^2 ))dx =∫_0 ^∞ (x^(((11)/4)−1) /((1+x^3 )^2 ))dx =((π(3−((11)/4)))/(9sin(((11π)/(12)))))=... ∫_0 ^∞ (x^(3/4) /((1+x^3 )^2 ))dx=∫_0 ^∞ (x^((7/4)−1) /((1+x^3 )^2 ))dx =((π(3−(7/4)))/(9sin(((7π)/(12)))))=...
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{−\frac{\mathrm{1}}{\mathrm{4}}} \left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\frac{\mathrm{7}}{\mathrm{4}}} +\mathrm{2}{x}^{\frac{\mathrm{3}}{\mathrm{4}}} \:+{x}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$$${let}\:\varphi\left({a},{b}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{a}−\mathrm{1}} }{{x}^{\mathrm{3}} +{b}^{\mathrm{3}} }{dx}\:\Rightarrow \\ $$$$\frac{\partial\varphi}{\partial{b}}=−\mathrm{3}{b}^{\mathrm{2}} \int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{{a}−\mathrm{1}} }{\left({x}^{\mathrm{3}} +{b}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{a}−\mathrm{1}} }{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}=−\frac{\mathrm{1}}{\mathrm{3}}\frac{\partial\varphi}{\partial{b}}\mid_{{b}=\mathrm{1}} \\ $$$$\varphi\left({a},{b}\right)=_{{x}={bz}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({bz}\right)^{{a}−\mathrm{1}} }{{b}^{\mathrm{3}} \left(\mathrm{1}+{z}^{\mathrm{3}} \right)}{b}\:{dz} \\ $$$$={b}^{{a}−\mathrm{3}} \int_{\mathrm{0}} ^{\infty} \:\:\frac{{z}^{{a}−\mathrm{1}} }{\mathrm{1}+{z}^{\mathrm{3}} }{dz}\:\:\:\:\:\left({z}^{\mathrm{3}} ={t}\right) \\ $$$$={b}^{{a}−\mathrm{3}} \int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\frac{{a}−\mathrm{1}}{\mathrm{3}}} }{\mathrm{1}+{t}}\frac{\mathrm{1}}{\mathrm{3}}{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{dt} \\ $$$$=\frac{{b}^{{a}−\mathrm{3}} }{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{{a}}{\mathrm{3}}−\mathrm{1}} }{\mathrm{1}+{t}}{dt} \\ $$$$=\frac{{b}^{{a}−\mathrm{3}} }{\mathrm{3}}×\frac{\pi}{{sin}\left(\frac{{a}\pi}{\mathrm{3}}\right)}\:\Rightarrow \\ $$$$\frac{\partial\varphi}{\partial{b}}\left({a},{b}\right)=\frac{\left({a}−\mathrm{3}\right.}{\mathrm{3}}{b}^{{a}−\mathrm{4}} \frac{\pi}{{sin}\left(\frac{{a}\pi}{\mathrm{3}}\right)}\:\Rightarrow \\ $$$$\frac{\partial\varphi}{\partial{b}}\mid_{{b}=\mathrm{1}} =\frac{{a}−\mathrm{3}}{\mathrm{3}}×\frac{\pi}{{sin}\left(\frac{\pi{a}}{\mathrm{3}}\right)} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}−\mathrm{1}} }{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}=\frac{\pi\left(\mathrm{3}−{a}\right)}{\mathrm{9}{sin}\left(\frac{\pi{a}}{\mathrm{3}}\right)} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\frac{\mathrm{7}}{\mathrm{4}}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx}\:\:\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\frac{\mathrm{11}}{\mathrm{4}}−\mathrm{1}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\pi\left(\mathrm{3}−\frac{\mathrm{11}}{\mathrm{4}}\right)}{\mathrm{9}{sin}\left(\frac{\mathrm{11}\pi}{\mathrm{12}}\right)}=… \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\frac{\mathrm{7}}{\mathrm{4}}−\mathrm{1}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\pi\left(\mathrm{3}−\frac{\mathrm{7}}{\mathrm{4}}\right)}{\mathrm{9}{sin}\left(\frac{\mathrm{7}\pi}{\mathrm{12}}\right)}=… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *