Question Number 168772 by Dildora last updated on 17/Apr/22

Commented by safojontoshtemirov last updated on 18/Apr/22
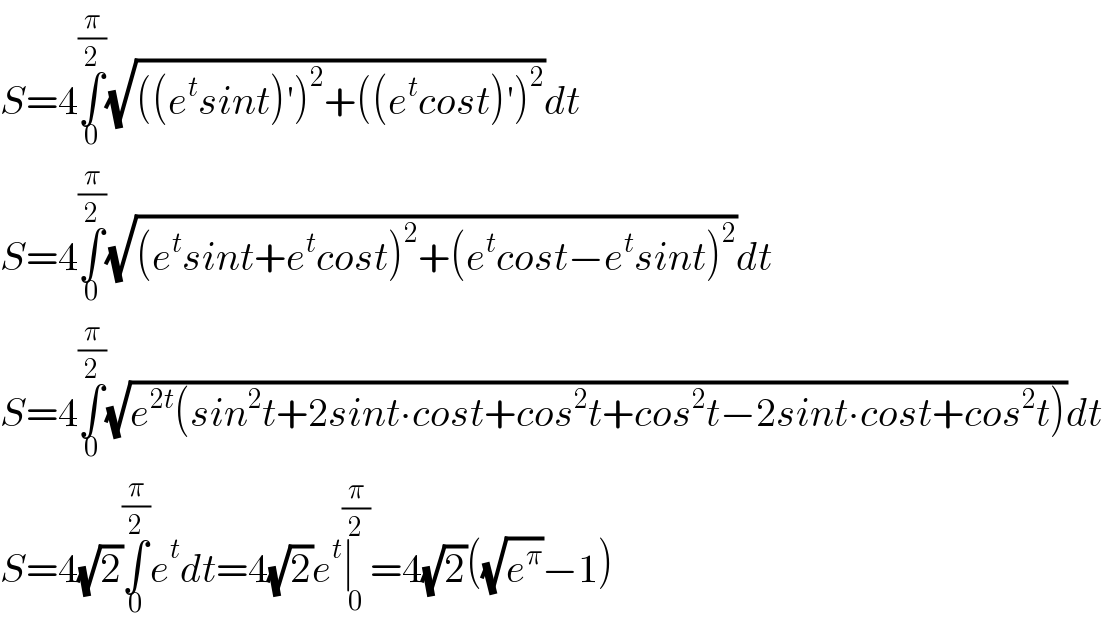
$${S}=\mathrm{4}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\sqrt{\left(\left({e}^{{t}} {sint}\right)'\right)^{\mathrm{2}} +\left(\left({e}^{{t}} {cost}\right)'\right)^{\mathrm{2}} }{dt}\: \\ $$$${S}=\mathrm{4}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\sqrt{\left({e}^{{t}} {sint}+{e}^{{t}} {cost}\right)^{\mathrm{2}} +\left({e}^{{t}} {cost}−{e}^{{t}} {sint}\right)^{\mathrm{2}} }{dt} \\ $$$${S}=\mathrm{4}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\sqrt{{e}^{\mathrm{2}{t}} \left({sin}^{\mathrm{2}} {t}+\mathrm{2}{sint}\centerdot{cost}+{cos}^{\mathrm{2}} {t}+{cos}^{\mathrm{2}} {t}−\mathrm{2}{sint}\centerdot{cost}+{cos}^{\mathrm{2}} {t}\right)}{dt} \\ $$$${S}=\mathrm{4}\sqrt{\mathrm{2}}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}{e}^{{t}} {dt}=\mathrm{4}\sqrt{\mathrm{2}}{e}^{{t}} \underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\mid}}=\mathrm{4}\sqrt{\mathrm{2}}\left(\sqrt{{e}^{\pi} }−\mathrm{1}\right) \\ $$
Answered by alephzero last updated on 17/Apr/22

$$ \: \: \: ??? \\ $$$$ \: \: \: \\ $$$$ \\ $$
Commented by Dildora last updated on 17/Apr/22

$${the}\:{volume}\:{of}\:{an}\:{object}\:{formed}\:{by}\:{rotating}\:{it}\:{around}\:{an}\:{axis} \\ $$
