Question Number 168813 by safojontoshtemirov last updated on 18/Apr/22
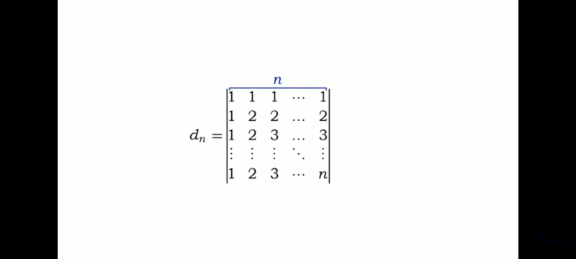
Answered by aleks041103 last updated on 18/Apr/22

$${We}\:{can}\:{add}\:{and}/{or}\:{subtract}\:{different} \\ $$$${rows}\:{from}\:{each}\:{other}\:{without}\:{changing} \\ $$$${the}\:{determinant}. \\ $$$$\Rightarrow{d}_{{n}} =\begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\ldots}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}}&{\ldots}&{\mathrm{2}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}&{\ldots}&{\mathrm{3}}&{\mathrm{3}}\\{\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}&{\ldots}&{{n}−\mathrm{1}}&{{n}−\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}&{\ldots}&{{n}−\mathrm{1}}&{{n}}\end{vmatrix} \\ $$$${subtracting}\:{the}\:\left({n}−\mathrm{1}\right){th}\:{row}\:{from}\:{the}\: \\ $$$${n}−{th}\:{row}\:{we}\:{get}: \\ $$$${d}_{{n}} =\begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\ldots}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}}&{\ldots}&{\mathrm{2}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}&{\ldots}&{\mathrm{3}}&{\mathrm{3}}\\{\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}&{\ldots}&{{n}−\mathrm{1}}&{{n}−\mathrm{1}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}&{\ldots}&{\mathrm{0}}&{\mathrm{1}}\end{vmatrix}= \\ $$$$=\left(−\mathrm{1}\right)^{\left({n}−\mathrm{1}\right)+\left({n}−\mathrm{1}\right)} \begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\ldots}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}}&{\ldots}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}&{\ldots}&{\mathrm{3}}\\{\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}&{\ldots}&{{n}−\mathrm{1}}\end{vmatrix}= \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{2}\left({n}−\mathrm{1}\right)} {d}_{{n}−\mathrm{1}} ={d}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{d}_{{n}} ={d}_{{n}−\mathrm{1}} \Rightarrow{d}_{{n}} ={d}_{\mathrm{1}} =\mid\mathrm{1}\mid \\ $$$$\Rightarrow{d}_{{n}} =\mathrm{1} \\ $$
