Menu Close

Question-168926

Tinku Tara 0 Comments
Pin




Question Number 168926 by mr W last updated on 22/Apr/22
Commented by mr W last updated on 22/Apr/22
M=midpoint of Aa L=midpoint of Bb K=midpoint of Cc prove 1. Δ_(abc) =4Δ_(MLK) 2. ab+bc+ca≤2(ML+LK+KM)
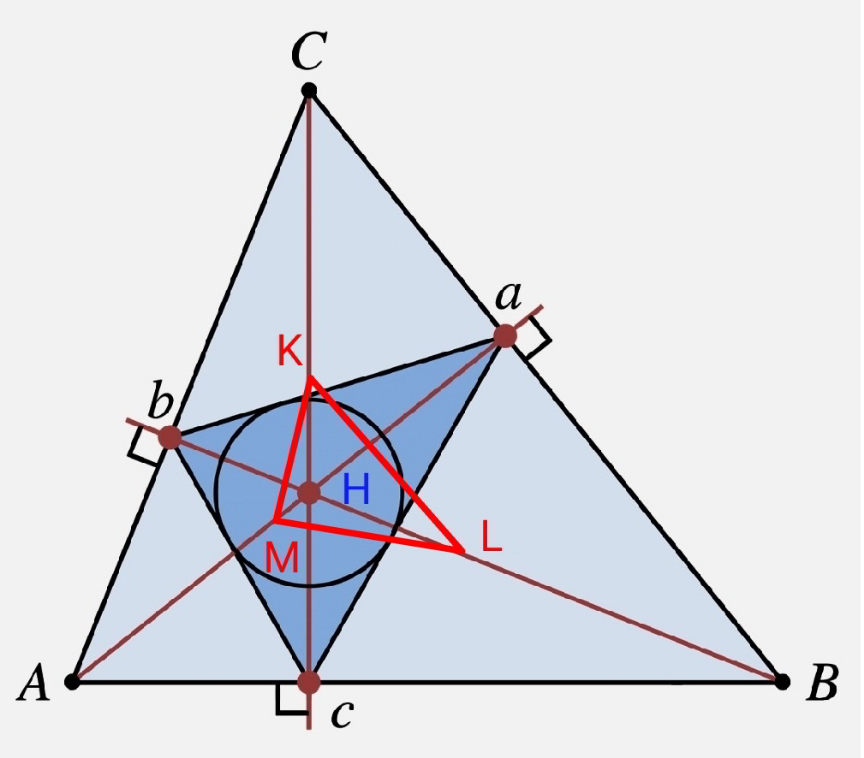
$${M}={midpoint}\:{of}\:{Aa} \\ $$$${L}={midpoint}\:{of}\:{Bb} \\ $$$${K}={midpoint}\:{of}\:{Cc} \\ $$$${prove}\: \\ $$$$\mathrm{1}.\:\Delta_{{abc}} =\mathrm{4}\Delta_{{MLK}} \\ $$$$\mathrm{2}.\:{ab}+{bc}+{ca}\leqslant\mathrm{2}\left({ML}+{LK}+{KM}\right) \\ $$
Commented by mr W last updated on 22/Apr/22
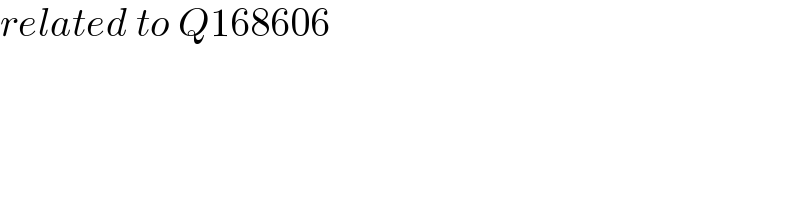
related to Q168606
$${related}\:{to}\:{Q}\mathrm{168606} \\ $$
Answered by mr W last updated on 22/Apr/22
Part I AH=((Ac)/(sin B))=((b cos A)/(sin B))=((2R sin B cos A)/(sin B))=2R cos A similarly BH=2R cos B CH=2R cos C Ha=((Ba)/(tan C))=((c cos B)/(tan C))=((2R sin C cos B)/(tan C))=2R cos B cos C similarly Hb=2R cos C cos A Hc=2R cos A cos B HM=AH−((AH+Ha)/2)=(1/2)(AH−Ha) =R(cos A−cos B cos C) HL=BH−((BH+Hb)/2)=(1/2)(BH−Hb) =R(cos B−cos C cos A) HK=CH−((CH+Hc)/2)=(1/2)(CH−Hc) =R(cos C−cos A cos B) 2Δ_(abc) =HM×HL×sin C+HL×HK×sin A+HK×HM×sin B 2Δ_(abc) =4R^2 (cos B cos C×cos C cos A×sin C+cos C cos A×cos A cos B×sin A+cos A cos B×cos B cos C×sin B) Δ_(abc) =R^2 cos A cos B cos C(sin 2A+sin 2B+sin 2C) Δ_(abc) =4R^2 cos A cos B cos C sin A sin B sin C ⇒Δ_(abc) =(R^2 /2) sin 2A sin 2B sin 2C 2Δ_(MLK) =HM×HL×sin C+HL×HK×sin A+HK×HM×sin B (2/R^2 )Δ_(MLK) =(cos A−cos B cos C)(cos B−cos C cos A)sin C+(cos B−cos C cos A)(cos C−cos A cos B)sin A+(cos C−cos A cos B)(cos A−cos B cos C)sin B (2/R^2 )Δ_(MLK) =cos A cos B cos C (tan A+tan B+tan C)−(1/2)(sin 2A+sin 2B+sin 2C)−(1/4)(cos 2A sin 2C+cos 2B sin 2C+cos 2B sin 2A+cos 2C sin 2A+cos 2C sin 2B+cos 2A sin 2B)+(1/2)cos A cos B cos C (sin 2A+sin 2B+sin 2C) (2/R^2 )Δ_(MLK) =cos A cos B cos C (tan A+tan B+tan C)−(1/2)(sin 2A+sin 2B+sin 2C)−(1/4)[sin 2(A+C)+sin 2(B+C)+ sin 2(A+B)]+(1/2)cos A cos B cos C (sin 2A+sin 2B+sin 2C) (2/R^2 )Δ_(MLK) =cos A cos B cos C tan A tan B tan C−(1/2)(sin 2A+sin 2B+sin 2C)+(1/4)(sin 2A+sin 2B+ sin 2C)+(1/2)cos A cos B cos C (sin 2A+sin 2B+sin 2C) (2/R^2 )Δ_(MLK) =sin A sin B sin C−sin A sin B sin C+2cos A cos B cos C sin A sin B sin C (2/R^2 )Δ_(MLK) =(1/4)sin 2A sin 2B sin 2C ⇒Δ_(MLK) =(R^2 /8)sin 2A sin 2B sin 2C ⇒Δ_(abc) =4Δ_(MLK)
$$\underline{\boldsymbol{{Part}}\:\boldsymbol{{I}}} \\ $$$${AH}=\frac{{Ac}}{\mathrm{sin}\:{B}}=\frac{{b}\:\mathrm{cos}\:{A}}{\mathrm{sin}\:{B}}=\frac{\mathrm{2}{R}\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{A}}{\mathrm{sin}\:{B}}=\mathrm{2}{R}\:\mathrm{cos}\:{A} \\ $$$${similarly} \\ $$$${BH}=\mathrm{2}{R}\:\mathrm{cos}\:{B} \\ $$$${CH}=\mathrm{2}{R}\:\mathrm{cos}\:{C} \\ $$$$ \\ $$$${Ha}=\frac{{Ba}}{\mathrm{tan}\:{C}}=\frac{{c}\:\mathrm{cos}\:{B}}{\mathrm{tan}\:{C}}=\frac{\mathrm{2}{R}\:\mathrm{sin}\:{C}\:\mathrm{cos}\:{B}}{\mathrm{tan}\:{C}}=\mathrm{2}{R}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C} \\ $$$${similarly} \\ $$$${Hb}=\mathrm{2}{R}\:\mathrm{cos}\:{C}\:\mathrm{cos}\:{A} \\ $$$${Hc}=\mathrm{2}{R}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{B} \\ $$$$ \\ $$$${HM}={AH}−\frac{{AH}+{Ha}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left({AH}−{Ha}\right) \\ $$$$={R}\left(\mathrm{cos}\:{A}−\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right) \\ $$$${HL}={BH}−\frac{{BH}+{Hb}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left({BH}−{Hb}\right) \\ $$$$={R}\left(\mathrm{cos}\:{B}−\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}\right) \\ $$$${HK}={CH}−\frac{{CH}+{Hc}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left({CH}−{Hc}\right) \\ $$$$={R}\left(\mathrm{cos}\:{C}−\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\right) \\ $$$$ \\ $$$$\mathrm{2}\Delta_{{abc}} ={HM}×{HL}×\mathrm{sin}\:{C}+{HL}×{HK}×\mathrm{sin}\:{A}+{HK}×{HM}×\mathrm{sin}\:{B} \\ $$$$\mathrm{2}\Delta_{{abc}} =\mathrm{4}{R}^{\mathrm{2}} \left(\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}×\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}×\mathrm{sin}\:{C}+\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}×\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}×\mathrm{sin}\:{A}+\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}×\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}×\mathrm{sin}\:{B}\right) \\ $$$$\Delta_{{abc}} ={R}^{\mathrm{2}} \mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right) \\ $$$$\Delta_{{abc}} =\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$\Rightarrow\Delta_{{abc}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}{A}\:\mathrm{sin}\:\mathrm{2}{B}\:\mathrm{sin}\:\mathrm{2}{C} \\ $$$$ \\ $$$$\mathrm{2}\Delta_{{MLK}} ={HM}×{HL}×\mathrm{sin}\:{C}+{HL}×{HK}×\mathrm{sin}\:{A}+{HK}×{HM}×\mathrm{sin}\:{B} \\ $$$$\frac{\mathrm{2}}{{R}^{\mathrm{2}} }\Delta_{{MLK}} =\left(\mathrm{cos}\:{A}−\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right)\left(\mathrm{cos}\:{B}−\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}\right)\mathrm{sin}\:{C}+\left(\mathrm{cos}\:{B}−\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}\right)\left(\mathrm{cos}\:{C}−\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\right)\mathrm{sin}\:{A}+\left(\mathrm{cos}\:{C}−\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\right)\left(\mathrm{cos}\:{A}−\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right)\mathrm{sin}\:{B} \\ $$$$\frac{\mathrm{2}}{{R}^{\mathrm{2}} }\Delta_{{MLK}} =\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\left(\mathrm{tan}\:{A}+\mathrm{tan}\:{B}+\mathrm{tan}\:{C}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{cos}\:\mathrm{2}{A}\:\mathrm{sin}\:\mathrm{2}{C}+\mathrm{cos}\:\mathrm{2}{B}\:\:\mathrm{sin}\:\mathrm{2}{C}+\mathrm{cos}\:\mathrm{2}{B}\:\mathrm{sin}\:\mathrm{2}{A}+\mathrm{cos}\:\mathrm{2}{C}\:\mathrm{sin}\:\mathrm{2}{A}+\mathrm{cos}\:\mathrm{2}{C}\:\mathrm{sin}\:\mathrm{2}{B}+\mathrm{cos}\:\mathrm{2}{A}\:\mathrm{sin}\:\mathrm{2}{B}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right) \\ $$$$\frac{\mathrm{2}}{{R}^{\mathrm{2}} }\Delta_{{MLK}} =\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\left(\mathrm{tan}\:{A}+\mathrm{tan}\:{B}+\mathrm{tan}\:{C}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{sin}\:\mathrm{2}\left({A}+{C}\right)+\mathrm{sin}\:\mathrm{2}\left({B}+{C}\right)+\:\mathrm{sin}\:\mathrm{2}\left({A}+{B}\right)\right]+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right) \\ $$$$\frac{\mathrm{2}}{{R}^{\mathrm{2}} }\Delta_{{MLK}} =\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}\:\mathrm{tan}\:{C}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\:\mathrm{sin}\:\mathrm{2}{C}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right) \\ $$$$\frac{\mathrm{2}}{{R}^{\mathrm{2}} }\Delta_{{MLK}} =\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}−\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}+\mathrm{2cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$\frac{\mathrm{2}}{{R}^{\mathrm{2}} }\Delta_{{MLK}} =\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{A}\:\mathrm{sin}\:\mathrm{2}{B}\:\mathrm{sin}\:\mathrm{2}{C} \\ $$$$\Rightarrow\Delta_{{MLK}} =\frac{{R}^{\mathrm{2}} }{\mathrm{8}}\mathrm{sin}\:\mathrm{2}{A}\:\mathrm{sin}\:\mathrm{2}{B}\:\mathrm{sin}\:\mathrm{2}{C} \\ $$$$\Rightarrow\Delta_{{abc}} =\mathrm{4}\Delta_{{MLK}} \\ $$
Commented by mr W last updated on 21/Apr/22
following theorems are used: (a/(sin A))=(b/(sin B))=(c/(sin C))=2R sin 2A+sin 2B+sin 2C=4 sin A sin B sin C tan A+tan B+tan C=tan A tan B tan C
$${following}\:{theorems}\:{are}\:{used}: \\ $$$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}}=\mathrm{2}{R} \\ $$$$\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}=\mathrm{4}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$\mathrm{tan}\:{A}+\mathrm{tan}\:{B}+\mathrm{tan}\:{C}=\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}\:\mathrm{tan}\:{C} \\ $$
Commented by Tawa11 last updated on 21/Apr/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 23/Apr/22
Part II Ca=b cos C=2R cos B cos C Cb=a cos C=2R cos A cos C (ab)^2 =(2R cos B cos C)^2 +(2R cos A cos C)^2 +2×2R cos B cos C×2R cos A cos C×cos C (((ab)^2 )/(4R^2 ))=(cos^2 A+cos^2 B+cos^2 C+2 cos A cos B cos C−cos^2 C)cos^2 C (((ab)^2 )/(4R^2 ))=(3−sin^2 A−sin^2 B−sin^2 C+2 cos A cos B cos C−cos^2 C)cos^2 C (((ab)^2 )/(4R^2 ))=sin^2 C cos^2 C ⇒ab=R sin 2C ab+bc+ca=R(sin 2A+sin 2B+sin 2C) ⇒ab+bc+ca=4R sin A sin B sin C LK^2 =R^2 (cos B−cos C cos A)^2 +R^2 (cos C−cos A cos B)^2 +2R^2 (cos B−cos C cos A)(cos C−cos A cos B)cos A ((LK^2 )/R^2 )=(cos B−cos C cos A)^2 +(cos C−cos A cos B)^2 +2(cos B−cos C cos A)(cos C−cos A cos B)cos A ((LK^2 )/R^2 )= sin^2 A(cos^2 B+cos^2 C−2 cos A cos B cos C) ((LK^2 )/R^2 )= sin^2 A(3−sin^2 A−sin^2 B−sin^2 C−2 cos A cos B cos C−cos^2 A) ((LK^2 )/R^2 )= sin^2 A(1−cos^2 A) ((LK^2 )/R^2 )= sin^4 A ⇒LK=R sin^2 A ML+LK+KM=R (sin^2 A+sin^2 B+sin^2 C) ≥R×3×(sin A sin B sin C)^(2/3) >3R sin A sin B sin C =(3/4)×4R sin A sin B sin C =(3/4)(ab+bc+ca) ⇒ab+bc+ca<(4/3)(ML+LK+KM)<2(ML+LK+KM)
$$\underline{\boldsymbol{{Part}}\:\boldsymbol{{II}}} \\ $$$${Ca}={b}\:\mathrm{cos}\:{C}=\mathrm{2}{R}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C} \\ $$$${Cb}={a}\:\mathrm{cos}\:{C}=\mathrm{2}{R}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{C} \\ $$$$\left({ab}\right)^{\mathrm{2}} =\left(\mathrm{2}{R}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right)^{\mathrm{2}} +\left(\mathrm{2}{R}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{C}\right)^{\mathrm{2}} +\mathrm{2}×\mathrm{2}{R}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}×\mathrm{2}{R}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{C}×\mathrm{cos}\:{C} \\ $$$$\frac{\left({ab}\right)^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }=\left(\mathrm{cos}^{\mathrm{2}} \:{A}+\mathrm{cos}^{\mathrm{2}} \:{B}+\mathrm{cos}^{\mathrm{2}} \:{C}+\mathrm{2}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}−\mathrm{cos}^{\mathrm{2}} \:{C}\right)\mathrm{cos}^{\mathrm{2}} \:{C} \\ $$$$\frac{\left({ab}\right)^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }=\left(\mathrm{3}−\mathrm{sin}^{\mathrm{2}} \:{A}−\mathrm{sin}^{\mathrm{2}} \:{B}−\mathrm{sin}^{\mathrm{2}} \:{C}+\mathrm{2}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}−\mathrm{cos}^{\mathrm{2}} \:{C}\right)\mathrm{cos}^{\mathrm{2}} \:{C} \\ $$$$\frac{\left({ab}\right)^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }=\mathrm{sin}^{\mathrm{2}} \:{C}\:\mathrm{cos}^{\mathrm{2}} \:{C} \\ $$$$\Rightarrow{ab}={R}\:\mathrm{sin}\:\mathrm{2}{C} \\ $$$${ab}+{bc}+{ca}={R}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right) \\ $$$$\Rightarrow{ab}+{bc}+{ca}=\mathrm{4}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$ \\ $$$${LK}^{\mathrm{2}} ={R}^{\mathrm{2}} \left(\mathrm{cos}\:{B}−\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} \left(\mathrm{cos}\:{C}−\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\right)^{\mathrm{2}} +\mathrm{2}{R}^{\mathrm{2}} \left(\mathrm{cos}\:{B}−\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}\right)\left(\mathrm{cos}\:{C}−\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\right)\mathrm{cos}\:{A} \\ $$$$\frac{{LK}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\left(\mathrm{cos}\:{B}−\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}\right)^{\mathrm{2}} +\left(\mathrm{cos}\:{C}−\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{cos}\:{B}−\mathrm{cos}\:{C}\:\mathrm{cos}\:{A}\right)\left(\mathrm{cos}\:{C}−\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\right)\mathrm{cos}\:{A} \\ $$$$\frac{{LK}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\:\mathrm{sin}^{\mathrm{2}} \:{A}\left(\mathrm{cos}^{\mathrm{2}} \:{B}+\mathrm{cos}^{\mathrm{2}} \:{C}−\mathrm{2}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right) \\ $$$$\frac{{LK}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\:\mathrm{sin}^{\mathrm{2}} \:{A}\left(\mathrm{3}−\mathrm{sin}^{\mathrm{2}} \:{A}−\mathrm{sin}^{\mathrm{2}} \:{B}−\mathrm{sin}^{\mathrm{2}} \:{C}−\mathrm{2}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}−\mathrm{cos}^{\mathrm{2}} \:{A}\right) \\ $$$$\frac{{LK}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\:\mathrm{sin}^{\mathrm{2}} \:{A}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{A}\right) \\ $$$$\frac{{LK}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\:\mathrm{sin}^{\mathrm{4}} \:{A} \\ $$$$\Rightarrow{LK}={R}\:\mathrm{sin}^{\mathrm{2}} \:{A} \\ $$$${ML}+{LK}+{KM}={R}\:\left(\mathrm{sin}^{\mathrm{2}} \:{A}+\mathrm{sin}^{\mathrm{2}} \:{B}+\mathrm{sin}^{\mathrm{2}} \:{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\geqslant{R}×\mathrm{3}×\left(\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:>\mathrm{3}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{4}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{4}}\left({ab}+{bc}+{ca}\right) \\ $$$$\Rightarrow{ab}+{bc}+{ca}<\frac{\mathrm{4}}{\mathrm{3}}\left({ML}+{LK}+{KM}\right)<\mathrm{2}\left({ML}+{LK}+{KM}\right) \\ $$
Commented by Shrinava last updated on 23/Apr/22
PERFECT DEAR SIR THANKS
$$\mathrm{PERFECT}\:\mathrm{DEAR}\:\mathrm{SIR}\:\mathrm{THANKS} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *