Menu Close

Question-168946

Tinku Tara 0 Comments
Pin




Question Number 168946 by bagjagugum123 last updated on 22/Apr/22
Commented by bagjagugum123 last updated on 22/Apr/22
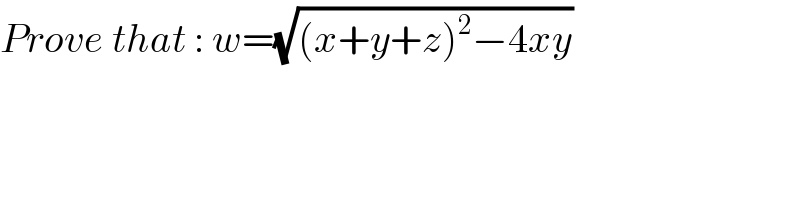
Prove that : w=(√((x+y+z)^2 −4xy))
$${Prove}\:{that}\::\:{w}=\sqrt{\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{4}{xy}} \\ $$
Answered by infinityaction last updated on 22/Apr/22
Commented by bagjagugum123 last updated on 22/Apr/22
Very nice, thank you Sir
$${Very}\:{nice},\:{thank}\:{you}\:{Sir} \\ $$
Answered by som(math1967) last updated on 22/Apr/22
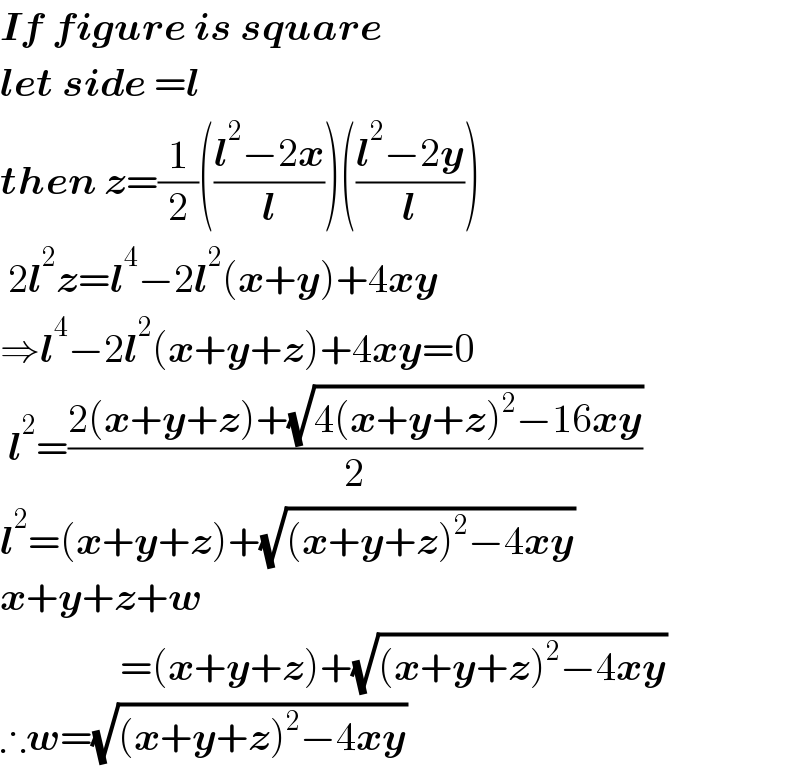
If figure is square let side =l then z=(1/2)(((l^2 −2x)/l))(((l^2 −2y)/l)) 2l^2 z=l^4 −2l^2 (x+y)+4xy ⇒l^4 −2l^2 (x+y+z)+4xy=0 l^2 =((2(x+y+z)+(√(4(x+y+z)^2 −16xy)))/2) l^2 =(x+y+z)+(√((x+y+z)^2 −4xy)) x+y+z+w =(x+y+z)+(√((x+y+z)^2 −4xy)) ∴w=(√((x+y+z)^2 −4xy))
$$\boldsymbol{{If}}\:\boldsymbol{{figure}}\:\boldsymbol{{is}}\:\boldsymbol{{square}} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{side}}\:=\boldsymbol{{l}} \\ $$$$\boldsymbol{{then}}\:\boldsymbol{{z}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\boldsymbol{{l}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{x}}}{\boldsymbol{{l}}}\right)\left(\frac{\boldsymbol{{l}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{y}}}{\boldsymbol{{l}}}\right) \\ $$$$\:\mathrm{2}\boldsymbol{{l}}^{\mathrm{2}} \boldsymbol{{z}}=\boldsymbol{{l}}^{\mathrm{4}} −\mathrm{2}\boldsymbol{{l}}^{\mathrm{2}} \left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)+\mathrm{4}\boldsymbol{{xy}} \\ $$$$\Rightarrow\boldsymbol{{l}}^{\mathrm{4}} −\mathrm{2}\boldsymbol{{l}}^{\mathrm{2}} \left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)+\mathrm{4}\boldsymbol{{xy}}=\mathrm{0} \\ $$$$\:\boldsymbol{{l}}^{\mathrm{2}} =\frac{\mathrm{2}\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)+\sqrt{\mathrm{4}\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)^{\mathrm{2}} −\mathrm{16}\boldsymbol{{xy}}}}{\mathrm{2}} \\ $$$$\boldsymbol{{l}}^{\mathrm{2}} =\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)+\sqrt{\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)^{\mathrm{2}} −\mathrm{4}\boldsymbol{{xy}}} \\ $$$$\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}+\boldsymbol{{w}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)+\sqrt{\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)^{\mathrm{2}} −\mathrm{4}\boldsymbol{{xy}}} \\ $$$$\therefore\boldsymbol{{w}}=\sqrt{\left(\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}\right)^{\mathrm{2}} −\mathrm{4}\boldsymbol{{xy}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *