Question-168982

Question Number 168982 by Tawa11 last updated on 22/Apr/22

Commented by mr W last updated on 22/Apr/22

$${all}\:{answers}\:{seem}\:{to}\:{be}\:{wrong}. \\ $$

Answered by mr W last updated on 22/Apr/22

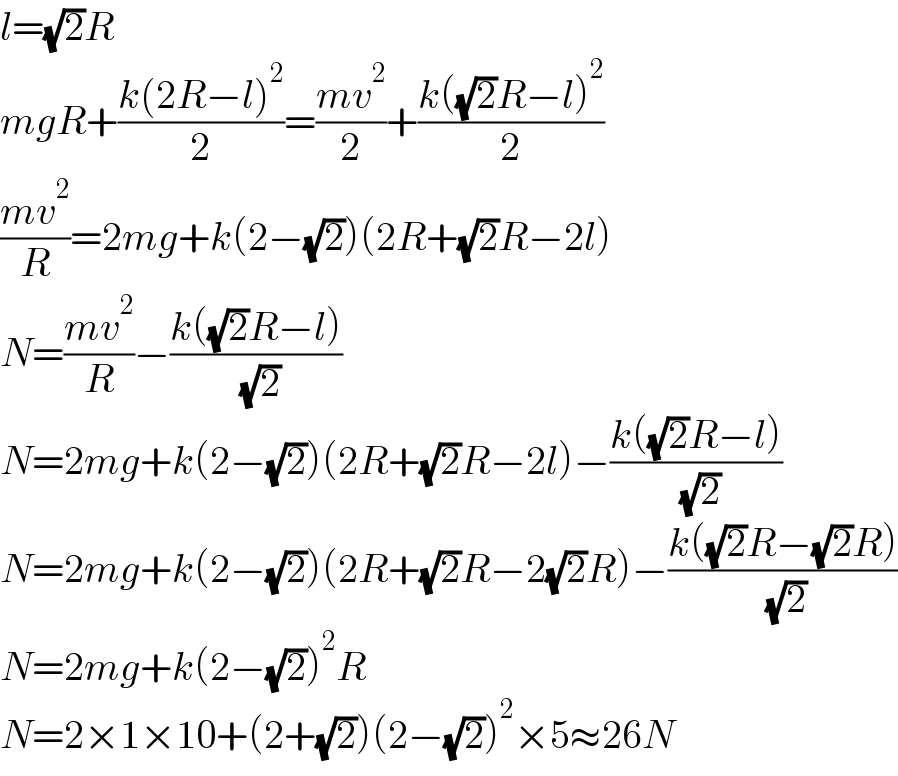
l=(√2)R mgR+((k(2R−l)^2 )/2)=((mv^2 )/2)+((k((√2)R−l)^2 )/2) ((mv^2 )/R)=2mg+k(2−(√2))(2R+(√2)R−2l) N=((mv^2 )/R)−((k((√2)R−l))/( (√2))) N=2mg+k(2−(√2))(2R+(√2)R−2l)−((k((√2)R−l))/( (√2))) N=2mg+k(2−(√2))(2R+(√2)R−2(√2)R)−((k((√2)R−(√2)R))/( (√2))) N=2mg+k(2−(√2))^2 R N=2×1×10+(2+(√2))(2−(√2))^2 ×5≈26N

$${l}=\sqrt{\mathrm{2}}{R} \\ $$$${mgR}+\frac{{k}\left(\mathrm{2}{R}−{l}\right)^{\mathrm{2}} }{\mathrm{2}}=\frac{{mv}^{\mathrm{2}} }{\mathrm{2}}+\frac{{k}\left(\sqrt{\mathrm{2}}{R}−{l}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{mv}^{\mathrm{2}} }{{R}}=\mathrm{2}{mg}+{k}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{2}{R}+\sqrt{\mathrm{2}}{R}−\mathrm{2}{l}\right) \\ $$$${N}=\frac{{mv}^{\mathrm{2}} }{{R}}−\frac{{k}\left(\sqrt{\mathrm{2}}{R}−{l}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$${N}=\mathrm{2}{mg}+{k}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{2}{R}+\sqrt{\mathrm{2}}{R}−\mathrm{2}{l}\right)−\frac{{k}\left(\sqrt{\mathrm{2}}{R}−{l}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$${N}=\mathrm{2}{mg}+{k}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{2}{R}+\sqrt{\mathrm{2}}{R}−\mathrm{2}\sqrt{\mathrm{2}}{R}\right)−\frac{{k}\left(\sqrt{\mathrm{2}}{R}−\sqrt{\mathrm{2}}{R}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$${N}=\mathrm{2}{mg}+{k}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} {R} \\ $$$${N}=\mathrm{2}×\mathrm{1}×\mathrm{10}+\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{5}\approx\mathrm{26}{N} \\ $$

Commented by mr W last updated on 23/Apr/22