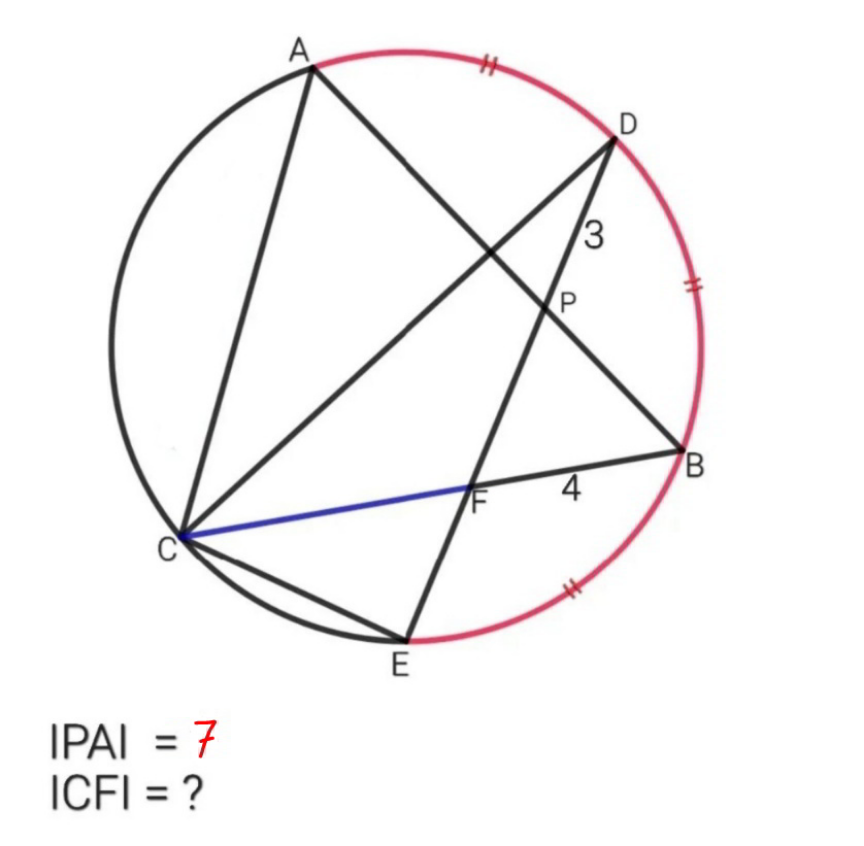
Question Number 169009 by mr W last updated on 23/Apr/22
Commented by mr W last updated on 23/Apr/22
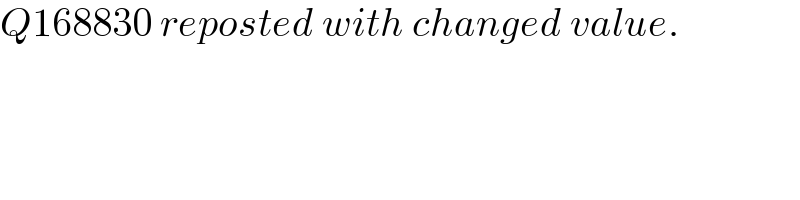
$${Q}\mathrm{168830}\:{reposted}\:{with}\:{changed}\:{value}. \\ $$
Commented by infinityaction last updated on 23/Apr/22
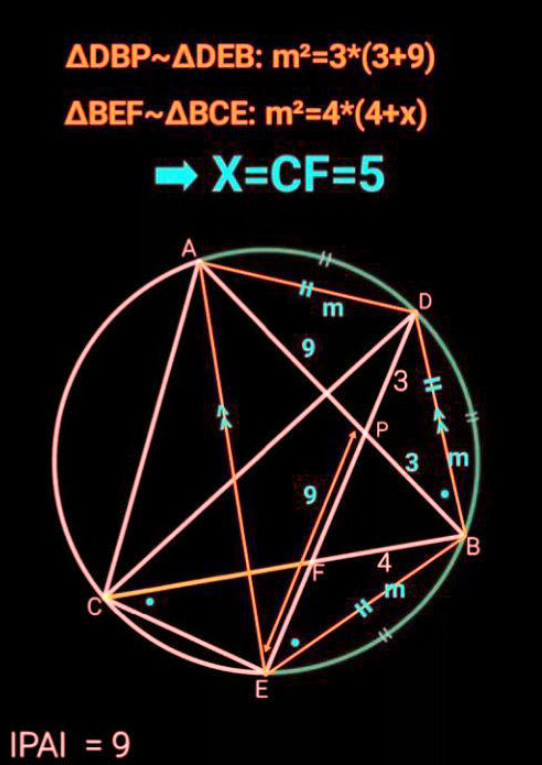
Commented by mr W last updated on 23/Apr/22
$${just}\:{think}! \\ $$$${m}^{\mathrm{2}} =\mathrm{3}×\left(\mathrm{3}+\mathrm{9}\right)=\mathrm{36}\:\Rightarrow{m}=\mathrm{6} \\ $$$${BD}={m}=\mathrm{6} \\ $$$$\Delta{PBD}\:{has}\:{side}\:{lengthes}\:\mathrm{3},\mathrm{6},\mathrm{3}.\: \\ $$$${and}\:{you}\:{think}\:{such}\:{a}\:{triangle}\:{is} \\ $$$${possible}? \\ $$$${that}'{s}\:{why}\:{i}\:{have}\:{changed}\:{to}\:\mid{PA}\mid=\mathrm{7}. \\ $$
Commented by mr W last updated on 23/Apr/22
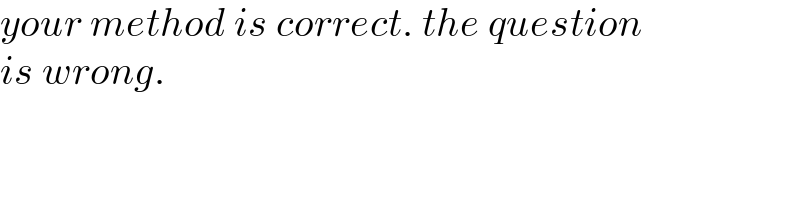
$${your}\:{method}\:{is}\:{correct}.\:{the}\:{question} \\ $$$${is}\:{wrong}. \\ $$
Commented by infinityaction last updated on 23/Apr/22

$${but}\:{sir}\:\mathrm{3},\mathrm{6},\mathrm{3}\:{is}\:{a}\:{possible}\:{tringle}\: \\ $$$${because}\:{this}\:{is}\:{a}\:{isosceles}\:{tringle} \\ $$
Commented by mr W last updated on 23/Apr/22
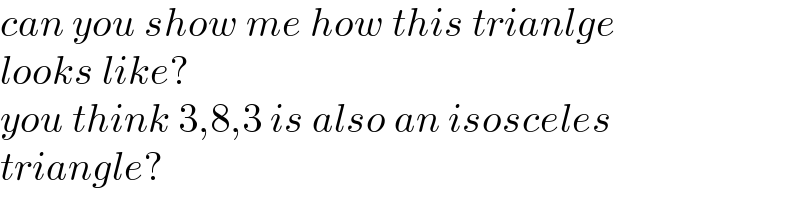
$${can}\:{you}\:{show}\:{me}\:{how}\:{this}\:{trianlge} \\ $$$${looks}\:{like}? \\ $$$${you}\:{think}\:\mathrm{3},\mathrm{8},\mathrm{3}\:{is}\:{also}\:{an}\:{isosceles} \\ $$$${triangle}? \\ $$
Commented by infinityaction last updated on 23/Apr/22
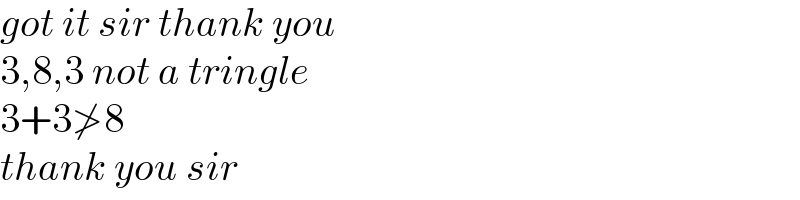
$${got}\:{it}\:{sir}\:{thank}\:{you} \\ $$$$\mathrm{3},\mathrm{8},\mathrm{3}\:{not}\:{a}\:{tringle} \\ $$$$\mathrm{3}+\mathrm{3}\ngtr\mathrm{8} \\ $$$${thank}\:{you}\:{sir} \\ $$
Commented by mr W last updated on 23/Apr/22

$${it}'{s}\:{alright}! \\ $$
Commented by ajfour last updated on 23/Apr/22
Commented by mr W last updated on 23/Apr/22

$${a}\:{good}\:{man}! \\ $$
Answered by mr W last updated on 23/Apr/22
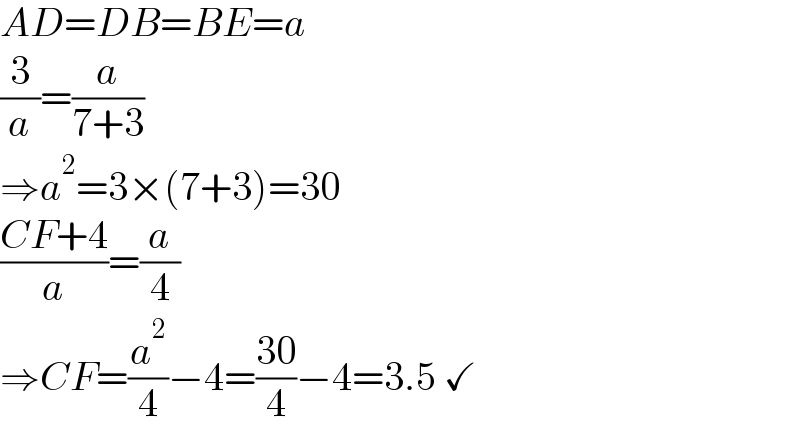
$${AD}={DB}={BE}={a} \\ $$$$\frac{\mathrm{3}}{{a}}=\frac{{a}}{\mathrm{7}+\mathrm{3}}\: \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\mathrm{3}×\left(\mathrm{7}+\mathrm{3}\right)=\mathrm{30} \\ $$$$\frac{{CF}+\mathrm{4}}{{a}}=\frac{{a}}{\mathrm{4}} \\ $$$$\Rightarrow{CF}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{4}=\frac{\mathrm{30}}{\mathrm{4}}−\mathrm{4}=\mathrm{3}.\mathrm{5}\:\checkmark \\ $$
Commented by Tawa11 last updated on 23/Apr/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
