Menu Close

Question-169013

Tinku Tara 0 Comments
Pin




Question Number 169013 by 0731619 last updated on 23/Apr/22
Commented by cortano1 last updated on 23/Apr/22
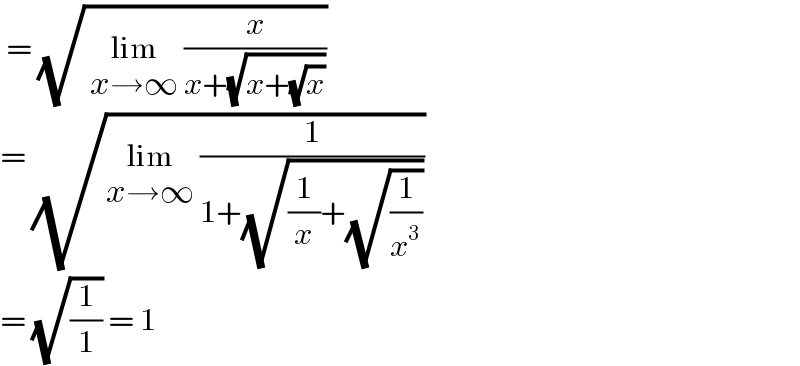
= (√( lim_(x→∞) (x/(x+(√(x+(√x))))))) = (√(lim_(x→∞) (1/(1+(√((1/x)+(√(1/x^3 )))))))) = (√(1/1)) = 1
$$\:=\:\sqrt{\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}}{{x}+\sqrt{{x}+\sqrt{{x}}}}}\: \\ $$$$=\:\sqrt{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{{x}}+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}}}} \\ $$$$=\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}\:=\:\mathrm{1} \\ $$
Answered by alephzero last updated on 23/Apr/22
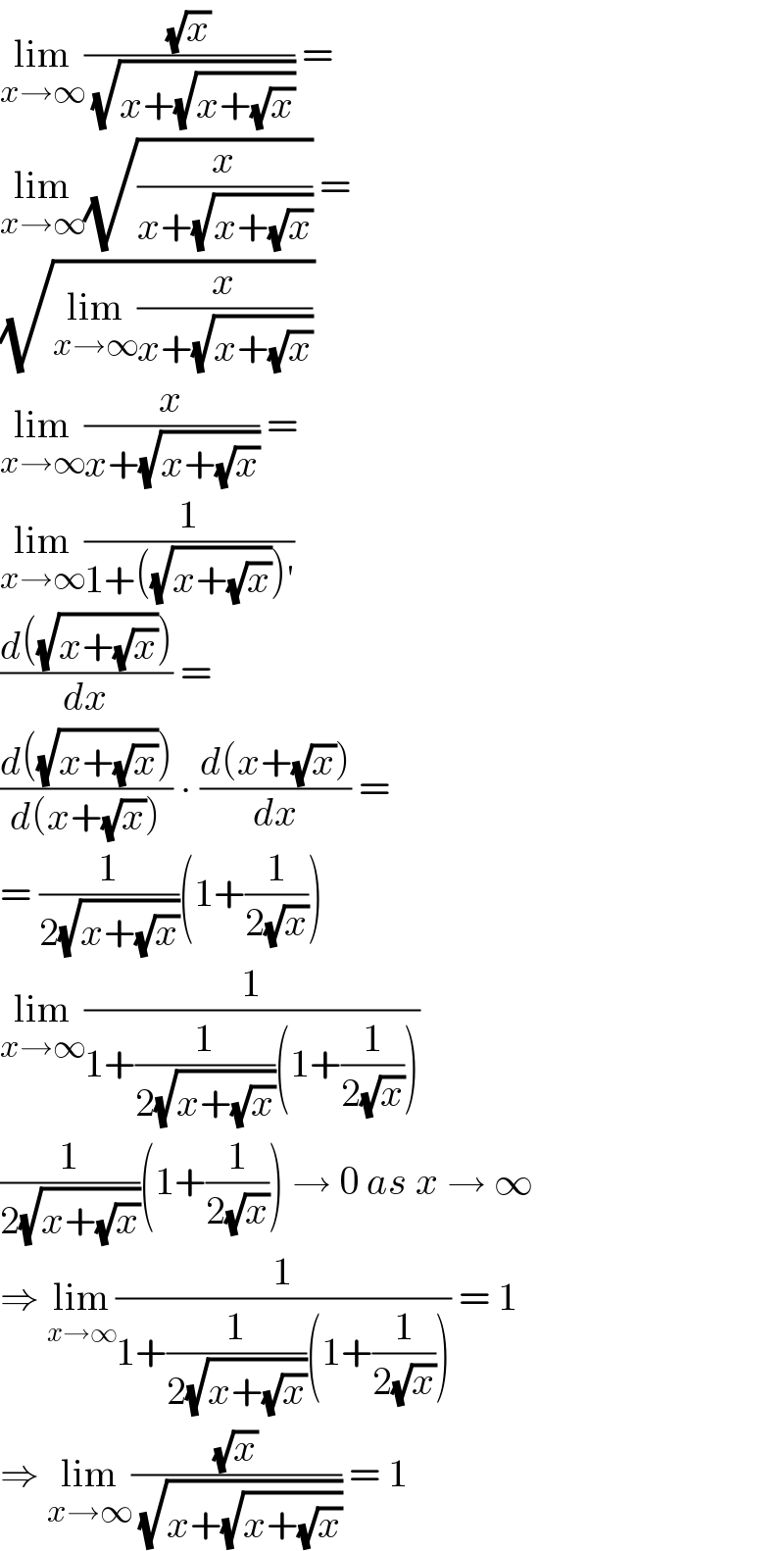
lim_(x→∞) ((√x)/( (√(x+(√(x+(√x))))))) = lim_(x→∞) (√(x/(x+(√(x+(√x)))))) = (√(lim_(x→∞) (x/(x+(√(x+(√x))))))) lim_(x→∞) (x/(x+(√(x+(√x))))) = lim_(x→∞) (1/(1+((√(x+(√x))))′)) ((d((√(x+(√x)))))/dx) = ((d((√(x+(√x)))))/(d(x+(√x)))) ∙ ((d(x+(√x)))/dx) = = (1/(2(√(x+(√x)))))(1+(1/(2(√x)))) lim_(x→∞) (1/(1+(1/(2(√(x+(√x)))))(1+(1/(2(√x)))))) (1/(2(√(x+(√x)))))(1+(1/(2(√x)))) → 0 as x → ∞ ⇒ lim_(x→∞) (1/(1+(1/(2(√(x+(√x)))))(1+(1/(2(√x)))))) = 1 ⇒ lim_(x→∞) ((√x)/( (√(x+(√(x+(√x))))))) = 1
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt{{x}}}{\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{\frac{{x}}{{x}+\sqrt{{x}+\sqrt{{x}}}}}\:= \\ $$$$\sqrt{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}}{{x}+\sqrt{{x}+\sqrt{{x}}}}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}}{{x}+\sqrt{{x}+\sqrt{{x}}}}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}+\left(\sqrt{{x}+\sqrt{{x}}}\right)'} \\ $$$$\frac{{d}\left(\sqrt{{x}+\sqrt{{x}}}\right)}{{dx}}\:= \\ $$$$\frac{{d}\left(\sqrt{{x}+\sqrt{{x}}}\right)}{{d}\left({x}+\sqrt{{x}}\right)}\:\centerdot\:\frac{{d}\left({x}+\sqrt{{x}}\right)}{{dx}}\:= \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right)\:\rightarrow\:\mathrm{0}\:{as}\:{x}\:\rightarrow\:\infty \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right)}\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt{{x}}}{\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}}\:=\:\mathrm{1} \\ $$
Answered by qaz last updated on 23/Apr/22
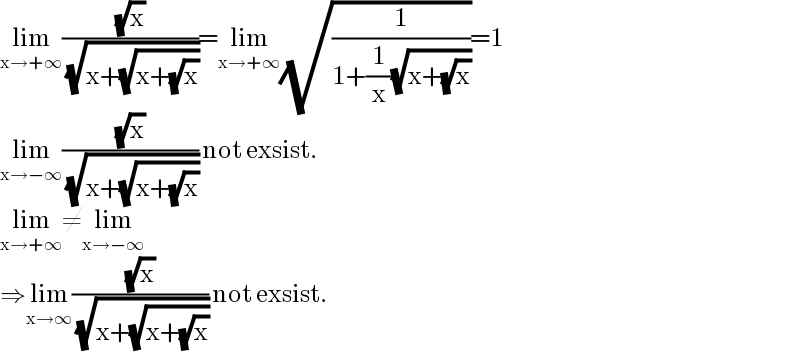
lim_(x→+∞) ((√x)/( (√(x+(√(x+(√x)))))))=lim_(x→+∞) (√(1/(1+(1/x)(√(x+(√x))))))=1 lim_(x→−∞) ((√x)/( (√(x+(√(x+(√x))))))) not exsist. lim_(x→+∞) ≠lim_(x→−∞) ⇒lim_(x→∞) ((√x)/( (√(x+(√(x+(√x))))))) not exsist.
$$\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}=\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}=\mathrm{1} \\ $$$$\underset{\mathrm{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}\:\mathrm{not}\:\mathrm{exsist}. \\ $$$$\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\neq\underset{\mathrm{x}\rightarrow−\infty} {\mathrm{lim}} \\ $$$$\Rightarrow\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}\:\mathrm{not}\:\mathrm{exsist}. \\ $$
Commented by JDamian last updated on 23/Apr/22
really, qaz? I hope you are not a math teacher
Commented by qaz last updated on 23/Apr/22
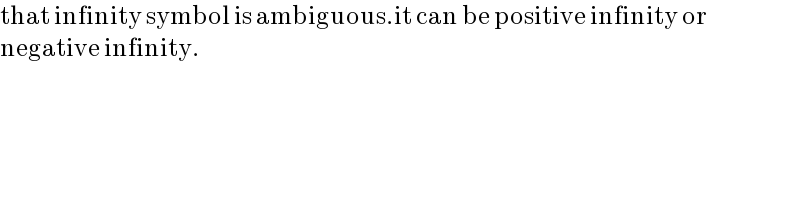
that infinity symbol is ambiguous.it can be positive infinity or negative infinity.
$$\mathrm{that}\:\mathrm{infinity}\:\mathrm{symbol}\:\mathrm{is}\:\mathrm{ambiguous}.\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{positive}\:\mathrm{infinity}\:\mathrm{or} \\ $$$$\mathrm{negative}\:\mathrm{infinity}. \\ $$
Commented by JDamian last updated on 23/Apr/22
so are ambiguous the symbols 1, 2, 3, ...
Commented by JDamian last updated on 23/Apr/22
According to your reasoning, lim_(x→∞) e^(−x) does not exist because lim_(x→−∞) e^(−x) ≠ lim_(x→+∞) e^(−x) , doesn′t it?
$${According}\:{to}\:{your}\:{reasoning},\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{e}^{−{x}} \:\:\:\:\:\:{does}\:{not}\:{exist}\:{because} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\:{e}^{−{x}} \:\neq\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\:{e}^{−{x}} ,\:{doesn}'{t}\:{it}? \\ $$
Commented by qaz last updated on 23/Apr/22
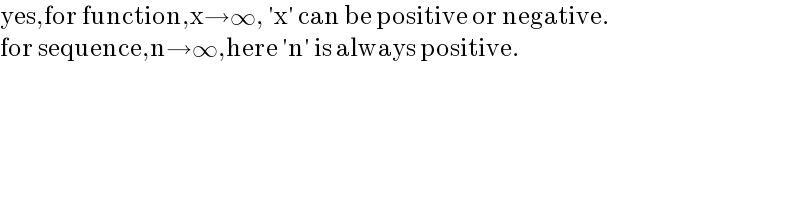
yes,for function,x→∞, ′x′ can be positive or negative. for sequence,n→∞,here ′n′ is always positive.
$$\mathrm{yes},\mathrm{for}\:\mathrm{function},\mathrm{x}\rightarrow\infty,\:'\mathrm{x}'\:\mathrm{can}\:\mathrm{be}\:\mathrm{positive}\:\mathrm{or}\:\mathrm{negative}. \\ $$$$\mathrm{for}\:\mathrm{sequence},\mathrm{n}\rightarrow\infty,\mathrm{here}\:'\mathrm{n}'\:\mathrm{is}\:\mathrm{always}\:\mathrm{positive}. \\ $$
Commented by JDamian last updated on 23/Apr/22
It is the first time I read that

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *