Question Number 169038 by mr W last updated on 23/Apr/22

Commented by mr W last updated on 23/Apr/22
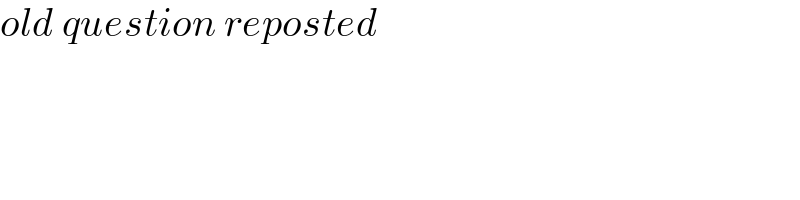
$${old}\:{question}\:{reposted} \\ $$
Answered by mr W last updated on 23/Apr/22

Commented by cortano1 last updated on 23/Apr/22

$${BC}\:{is}\:{diameter}? \\ $$
Commented by mr W last updated on 23/Apr/22
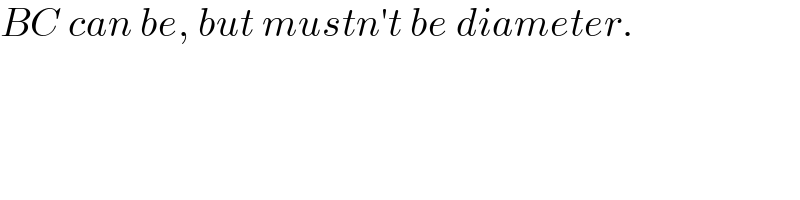
$${BC}\:{can}\:{be},\:{but}\:{mustn}'{t}\:{be}\:{diameter}. \\ $$
Commented by mr W last updated on 23/Apr/22
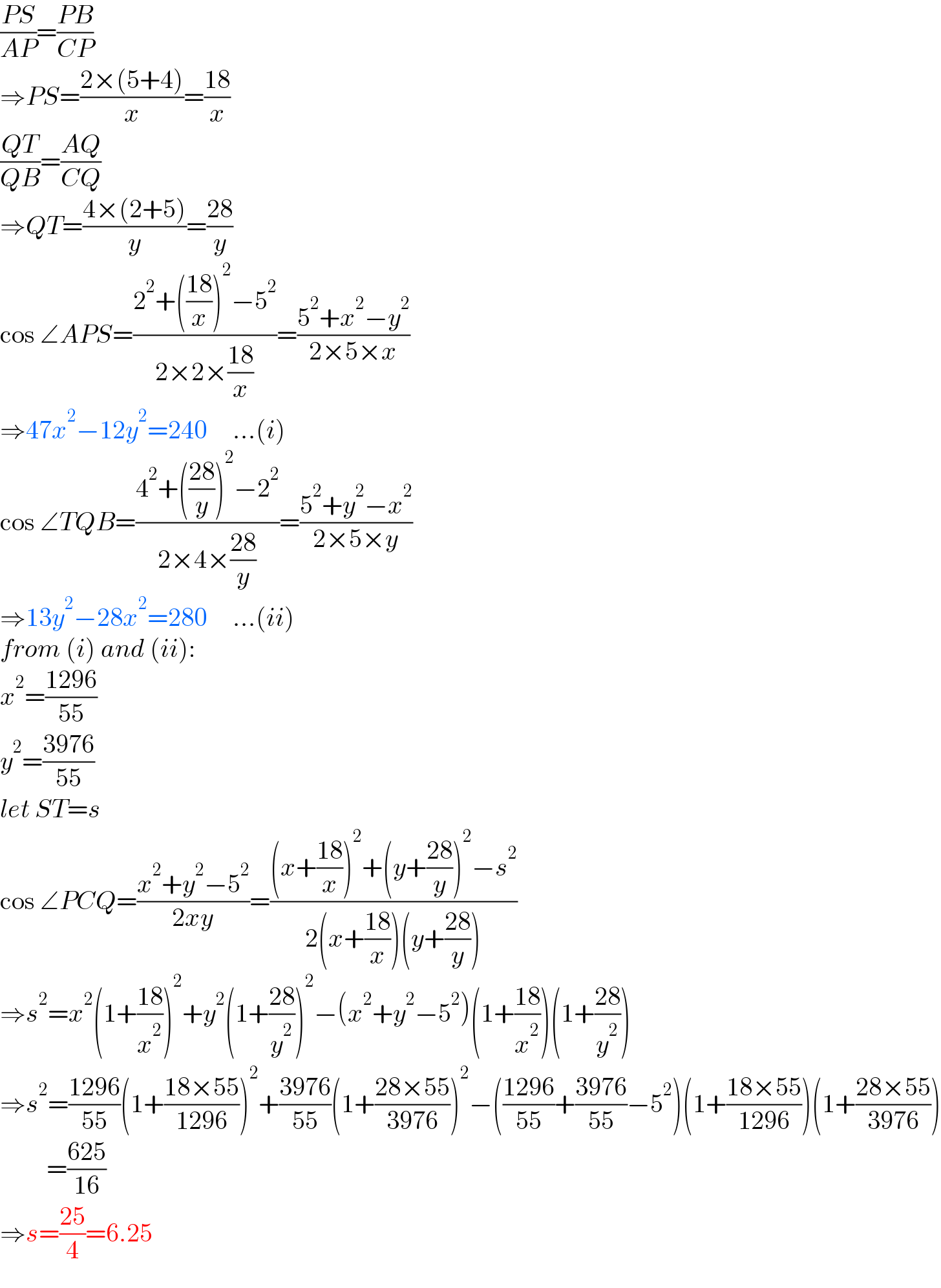
$$\frac{{PS}}{{AP}}=\frac{{PB}}{{CP}} \\ $$$$\Rightarrow{PS}=\frac{\mathrm{2}×\left(\mathrm{5}+\mathrm{4}\right)}{{x}}=\frac{\mathrm{18}}{{x}} \\ $$$$\frac{{QT}}{{QB}}=\frac{{AQ}}{{CQ}} \\ $$$$\Rightarrow{QT}=\frac{\mathrm{4}×\left(\mathrm{2}+\mathrm{5}\right)}{{y}}=\frac{\mathrm{28}}{{y}} \\ $$$$\mathrm{cos}\:\angle{APS}=\frac{\mathrm{2}^{\mathrm{2}} +\left(\frac{\mathrm{18}}{{x}}\right)^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}×\frac{\mathrm{18}}{{x}}}=\frac{\mathrm{5}^{\mathrm{2}} +{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{\mathrm{2}×\mathrm{5}×{x}} \\ $$$$\Rightarrow\mathrm{47}{x}^{\mathrm{2}} −\mathrm{12}{y}^{\mathrm{2}} =\mathrm{240}\:\:\:\:\:…\left({i}\right) \\ $$$$\mathrm{cos}\:\angle{TQB}=\frac{\mathrm{4}^{\mathrm{2}} +\left(\frac{\mathrm{28}}{{y}}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }{\mathrm{2}×\mathrm{4}×\frac{\mathrm{28}}{{y}}}=\frac{\mathrm{5}^{\mathrm{2}} +{y}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\mathrm{2}×\mathrm{5}×{y}} \\ $$$$\Rightarrow\mathrm{13}{y}^{\mathrm{2}} −\mathrm{28}{x}^{\mathrm{2}} =\mathrm{280}\:\:\:\:\:…\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{1296}}{\mathrm{55}}\: \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{3976}}{\mathrm{55}} \\ $$$${let}\:{ST}={s} \\ $$$$\mathrm{cos}\:\angle{PCQ}=\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}{xy}}=\frac{\left({x}+\frac{\mathrm{18}}{{x}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{28}}{{y}}\right)^{\mathrm{2}} −{s}^{\mathrm{2}} }{\mathrm{2}\left({x}+\frac{\mathrm{18}}{{x}}\right)\left({y}+\frac{\mathrm{28}}{{y}}\right)} \\ $$$$\Rightarrow{s}^{\mathrm{2}} ={x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{18}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{28}}{{y}^{\mathrm{2}} }\right)^{\mathrm{2}} −\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{18}}{{x}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{28}}{{y}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{s}^{\mathrm{2}} =\frac{\mathrm{1296}}{\mathrm{55}}\left(\mathrm{1}+\frac{\mathrm{18}×\mathrm{55}}{\mathrm{1296}}\right)^{\mathrm{2}} +\frac{\mathrm{3976}}{\mathrm{55}}\left(\mathrm{1}+\frac{\mathrm{28}×\mathrm{55}}{\mathrm{3976}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1296}}{\mathrm{55}}+\frac{\mathrm{3976}}{\mathrm{55}}−\mathrm{5}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{18}×\mathrm{55}}{\mathrm{1296}}\right)\left(\mathrm{1}+\frac{\mathrm{28}×\mathrm{55}}{\mathrm{3976}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{625}}{\mathrm{16}} \\ $$$$\Rightarrow{s}=\frac{\mathrm{25}}{\mathrm{4}}=\mathrm{6}.\mathrm{25} \\ $$
Commented by Tawa11 last updated on 23/Apr/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 24/Apr/22

