Question-169112

Question Number 169112 by mokys last updated on 24/Apr/22

Commented by aleks041103 last updated on 24/Apr/22

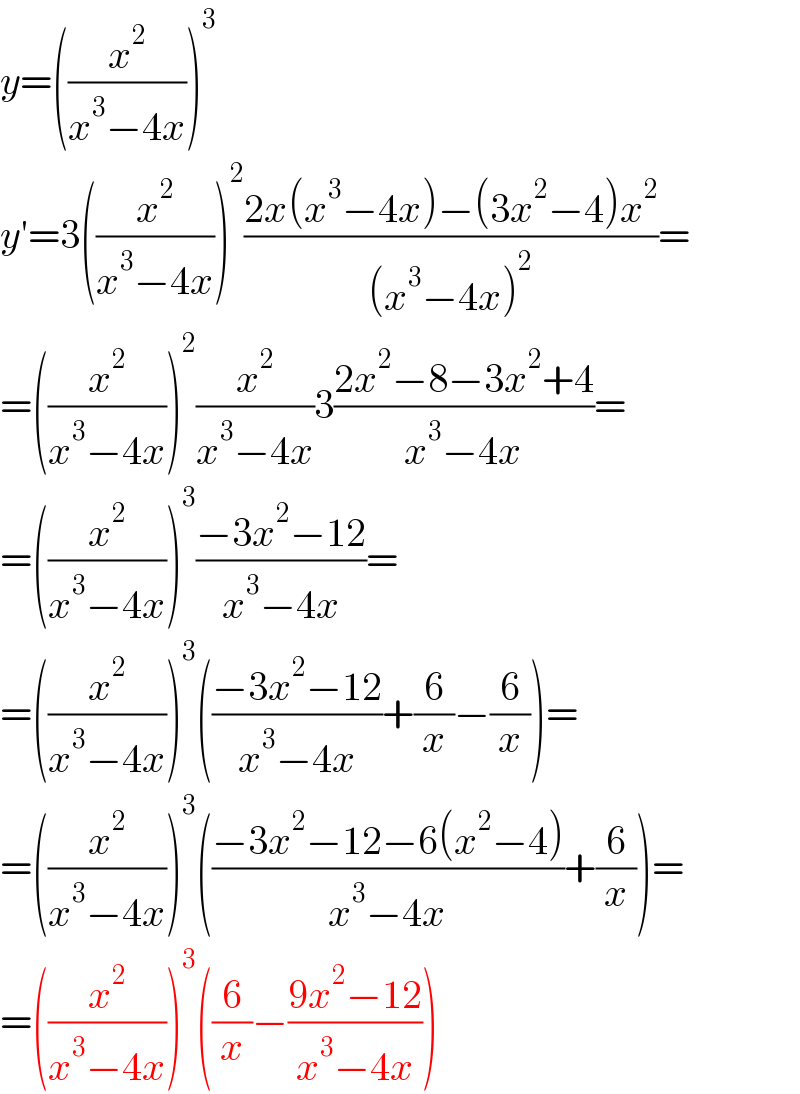
y=((x^2 /(x^3 −4x)))^3 y′=3((x^2 /(x^3 −4x)))^2 ((2x(x^3 −4x)−(3x^2 −4)x^2 )/((x^3 −4x)^2 ))= =((x^2 /(x^3 −4x)))^2 (x^2 /(x^3 −4x))3((2x^2 −8−3x^2 +4)/(x^3 −4x))= =((x^2 /(x^3 −4x)))^3 ((−3x^2 −12)/(x^3 −4x))= =((x^2 /(x^3 −4x)))^3 (((−3x^2 −12)/(x^3 −4x))+(6/x)−(6/x))= =((x^2 /(x^3 −4x)))^3 (((−3x^2 −12−6(x^2 −4))/(x^3 −4x))+(6/x))= =((x^2 /(x^3 −4x)))^3 ((6/x)−((9x^2 −12)/(x^3 −4x)))

$${y}=\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{3}} \\ $$$${y}'=\mathrm{3}\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{2}} \frac{\mathrm{2}{x}\left({x}^{\mathrm{3}} −\mathrm{4}{x}\right)−\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}\right){x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} −\mathrm{4}{x}\right)^{\mathrm{2}} }= \\ $$$$=\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{2}} \frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\mathrm{3}\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}}{{x}^{\mathrm{3}} −\mathrm{4}{x}}= \\ $$$$=\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{3}} \frac{−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}}{{x}^{\mathrm{3}} −\mathrm{4}{x}}= \\ $$$$=\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{3}} \left(\frac{−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}}{{x}^{\mathrm{3}} −\mathrm{4}{x}}+\frac{\mathrm{6}}{{x}}−\frac{\mathrm{6}}{{x}}\right)= \\ $$$$=\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{3}} \left(\frac{−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}−\mathrm{6}\left({x}^{\mathrm{2}} −\mathrm{4}\right)}{{x}^{\mathrm{3}} −\mathrm{4}{x}}+\frac{\mathrm{6}}{{x}}\right)= \\ $$$$=\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{3}} \left(\frac{\mathrm{6}}{{x}}−\frac{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{12}}{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right) \\ $$

Answered by greougoury555 last updated on 24/Apr/22

y = ((x^2 /(x^3 −4x)))^3 ⇒ln y = 3 [ ln (x^2 )−ln (x^3 −4x)] ⇒ln y = 6ln x−3ln (x^3 −4x) ⇒((y′)/y) = (6/x) −((3(3x^2 −4))/(x^3 −4x)) ⇒ (dy/dx) = ((6/x)−((9x^2 −12)/(x^3 −4x)))((x^2 /(x^3 −4x)))^3 ××××××××××××××

$$\:{y}\:=\:\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{3}} \\ $$$$\:\Rightarrow\mathrm{ln}\:{y}\:=\:\mathrm{3}\:\left[\:\mathrm{ln}\:\left({x}^{\mathrm{2}} \right)−\mathrm{ln}\:\left({x}^{\mathrm{3}} −\mathrm{4}{x}\right)\right] \\ $$$$\:\Rightarrow\mathrm{ln}\:{y}\:=\:\mathrm{6ln}\:{x}−\mathrm{3ln}\:\left({x}^{\mathrm{3}} −\mathrm{4}{x}\right) \\ $$$$\Rightarrow\frac{{y}'}{{y}}\:=\:\frac{\mathrm{6}}{{x}}\:−\frac{\mathrm{3}\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}\right)}{{x}^{\mathrm{3}} −\mathrm{4}{x}} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\left(\frac{\mathrm{6}}{{x}}−\frac{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{12}}{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{4}{x}}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:×××××××××××××× \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply