Question Number 169200 by Mastermind last updated on 25/Apr/22
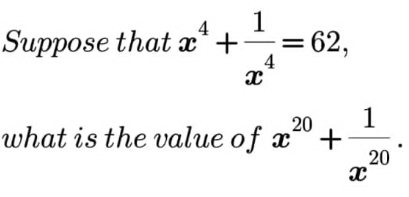
Answered by Rasheed.Sindhi last updated on 26/Apr/22
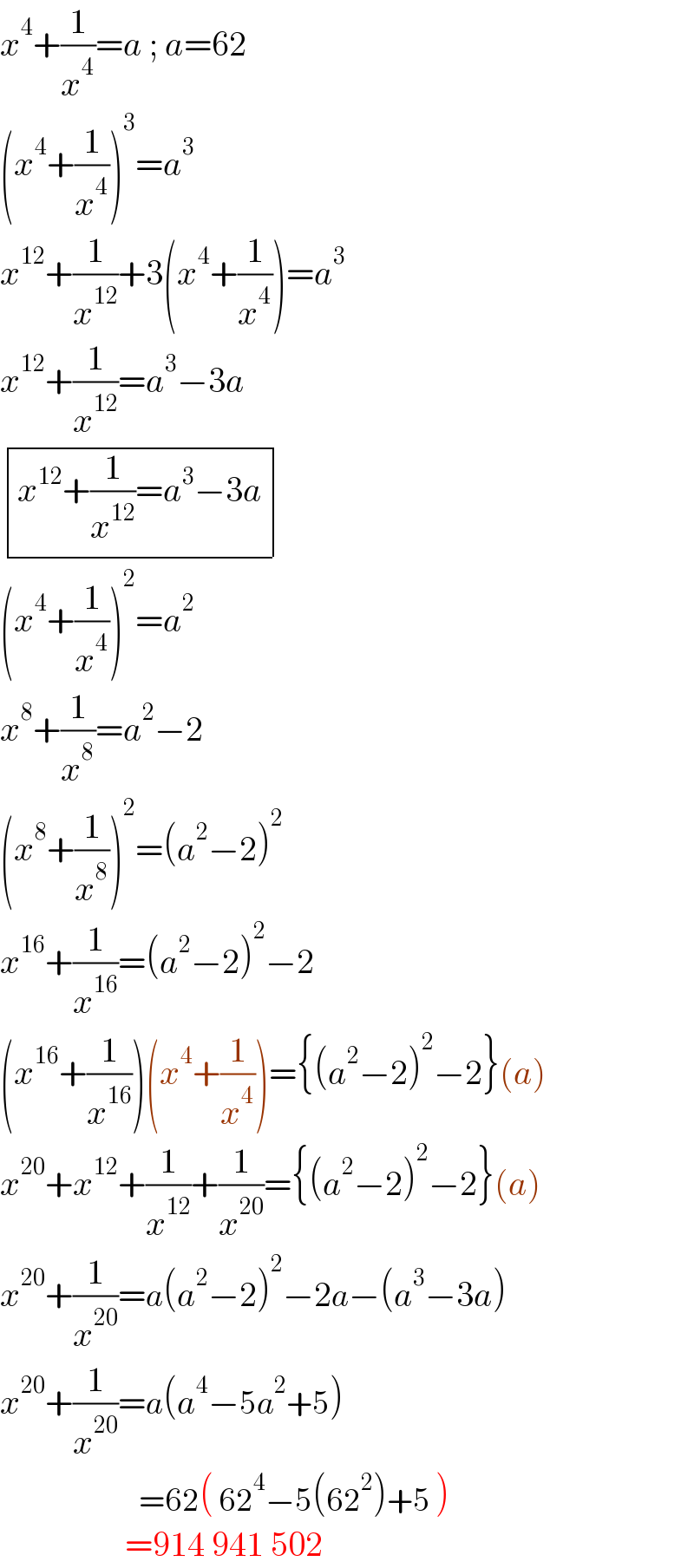
$${x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }={a}\:;\:{a}=\mathrm{62} \\ $$$$\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)^{\mathrm{3}} ={a}^{\mathrm{3}} \\ $$$${x}^{\mathrm{12}} +\frac{\mathrm{1}}{{x}^{\mathrm{12}} }+\mathrm{3}\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)={a}^{\mathrm{3}} \\ $$$${x}^{\mathrm{12}} +\frac{\mathrm{1}}{{x}^{\mathrm{12}} }={a}^{\mathrm{3}} −\mathrm{3}{a} \\ $$$$\begin{array}{|c|}{{x}^{\mathrm{12}} +\frac{\mathrm{1}}{{x}^{\mathrm{12}} }={a}^{\mathrm{3}} −\mathrm{3}{a}}\\\hline\end{array} \\ $$$$\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${x}^{\mathrm{8}} +\frac{\mathrm{1}}{{x}^{\mathrm{8}} }={a}^{\mathrm{2}} −\mathrm{2} \\ $$$$\left({x}^{\mathrm{8}} +\frac{\mathrm{1}}{{x}^{\mathrm{8}} }\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{16}} +\frac{\mathrm{1}}{{x}^{\mathrm{16}} }=\left({a}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\left({x}^{\mathrm{16}} +\frac{\mathrm{1}}{{x}^{\mathrm{16}} }\right)\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)=\left\{\left({a}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\right\}\left({a}\right) \\ $$$${x}^{\mathrm{20}} +{x}^{\mathrm{12}} +\frac{\mathrm{1}}{{x}^{\mathrm{12}} }+\frac{\mathrm{1}}{{x}^{\mathrm{20}} }=\left\{\left({a}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\right\}\left({a}\right) \\ $$$${x}^{\mathrm{20}} +\frac{\mathrm{1}}{{x}^{\mathrm{20}} }={a}\left({a}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}{a}−\left({a}^{\mathrm{3}} −\mathrm{3}{a}\right) \\ $$$${x}^{\mathrm{20}} +\frac{\mathrm{1}}{{x}^{\mathrm{20}} }={a}\left({a}^{\mathrm{4}} −\mathrm{5}{a}^{\mathrm{2}} +\mathrm{5}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{62}\left(\:\mathrm{62}^{\mathrm{4}} −\mathrm{5}\left(\mathrm{62}^{\mathrm{2}} \right)+\mathrm{5}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{914}\:\mathrm{941}\:\mathrm{502} \\ $$
Commented by Tawa11 last updated on 26/Apr/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 26/Apr/22
![t=x^4 METHOD 1: p_1 =e_1 =t+(1/t)=a=62 e_2 =t×(1/t)=1 p_2 =e_1 p_1 −2e_2 =a^2 −2 p_3 =e_1 p_2 −e_2 p_1 =a(a^2 −2)−a=a^3 −3a p_4 =e_1 p_3 −e_2 p_2 =a(a^3 −3a)−a^2 +2=a^4 −4a^2 +2 p_5 =e_1 p_4 −e_2 p_3 =a^5 −4a^3 +2a−a^3 +3a=a[(a^4 −2)(a^2 −3)−1] METHOD 2 t+(1/t)=a=62 (t+(1/t))^2 =t^2 +(1/t^2 )+2=a^2 ⇒t^2 +(1/t^2 )=a^2 −2 (t+(1/t))^3 =t^3 +(1/t^3 )+3(t+(1/t))=a^3 ⇒t^3 +(1/t^3 )=a^3 −3a (t^2 +(1/t^2 ))(t^3 +(1/t^3 ))=t^5 +(1/t^5 )+t+(1/t)=(a^2 −2)(a^3 −3a) ⇒t^5 +(1/t^5 )=(a^2 −2)(a^3 −3a)−a=a[(a^2 −2)(a^2 −3)−1] x^(20) +(1/x^(20) )=t^5 +(1/t^5 )=a[(a^2 −2)(a^2 −3)−1] =62[(62^2 −2)(62^2 −3)−1] =914 941 502](https://www.tinkutara.com/question/Q169203.png)
$${t}={x}^{\mathrm{4}} \\ $$$${METHOD}\:\mathrm{1}: \\ $$$${p}_{\mathrm{1}} ={e}_{\mathrm{1}} ={t}+\frac{\mathrm{1}}{{t}}={a}=\mathrm{62} \\ $$$${e}_{\mathrm{2}} ={t}×\frac{\mathrm{1}}{{t}}=\mathrm{1} \\ $$$${p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} ={a}^{\mathrm{2}} −\mathrm{2} \\ $$$${p}_{\mathrm{3}} ={e}_{\mathrm{1}} {p}_{\mathrm{2}} −{e}_{\mathrm{2}} {p}_{\mathrm{1}} ={a}\left({a}^{\mathrm{2}} −\mathrm{2}\right)−{a}={a}^{\mathrm{3}} −\mathrm{3}{a} \\ $$$${p}_{\mathrm{4}} ={e}_{\mathrm{1}} {p}_{\mathrm{3}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} ={a}\left({a}^{\mathrm{3}} −\mathrm{3}{a}\right)−{a}^{\mathrm{2}} +\mathrm{2}={a}^{\mathrm{4}} −\mathrm{4}{a}^{\mathrm{2}} +\mathrm{2} \\ $$$${p}_{\mathrm{5}} ={e}_{\mathrm{1}} {p}_{\mathrm{4}} −{e}_{\mathrm{2}} {p}_{\mathrm{3}} ={a}^{\mathrm{5}} −\mathrm{4}{a}^{\mathrm{3}} +\mathrm{2}{a}−{a}^{\mathrm{3}} +\mathrm{3}{a}={a}\left[\left({a}^{\mathrm{4}} −\mathrm{2}\right)\left({a}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{1}\right] \\ $$$$ \\ $$$${METHOD}\:\mathrm{2} \\ $$$${t}+\frac{\mathrm{1}}{{t}}={a}=\mathrm{62} \\ $$$$\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} ={t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{2}={a}^{\mathrm{2}} \\ $$$$\Rightarrow{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }={a}^{\mathrm{2}} −\mathrm{2} \\ $$$$\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{3}} ={t}^{\mathrm{3}} +\frac{\mathrm{1}}{{t}^{\mathrm{3}} }+\mathrm{3}\left({t}+\frac{\mathrm{1}}{{t}}\right)={a}^{\mathrm{3}} \\ $$$$\Rightarrow{t}^{\mathrm{3}} +\frac{\mathrm{1}}{{t}^{\mathrm{3}} }={a}^{\mathrm{3}} −\mathrm{3}{a} \\ $$$$\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\left({t}^{\mathrm{3}} +\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\right)={t}^{\mathrm{5}} +\frac{\mathrm{1}}{{t}^{\mathrm{5}} }+{t}+\frac{\mathrm{1}}{{t}}=\left({a}^{\mathrm{2}} −\mathrm{2}\right)\left({a}^{\mathrm{3}} −\mathrm{3}{a}\right) \\ $$$$\Rightarrow{t}^{\mathrm{5}} +\frac{\mathrm{1}}{{t}^{\mathrm{5}} }=\left({a}^{\mathrm{2}} −\mathrm{2}\right)\left({a}^{\mathrm{3}} −\mathrm{3}{a}\right)−{a}={a}\left[\left({a}^{\mathrm{2}} −\mathrm{2}\right)\left({a}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{1}\right] \\ $$$$ \\ $$$${x}^{\mathrm{20}} +\frac{\mathrm{1}}{{x}^{\mathrm{20}} }={t}^{\mathrm{5}} +\frac{\mathrm{1}}{{t}^{\mathrm{5}} }={a}\left[\left({a}^{\mathrm{2}} −\mathrm{2}\right)\left({a}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{1}\right] \\ $$$$=\mathrm{62}\left[\left(\mathrm{62}^{\mathrm{2}} −\mathrm{2}\right)\left(\mathrm{62}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{1}\right] \\ $$$$=\mathrm{914}\:\mathrm{941}\:\mathrm{502} \\ $$
Commented by Tawa11 last updated on 26/Apr/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
