Menu Close

Question-169230

Tinku Tara 0 Comments
Pin




Question Number 169230 by Giantyusuf last updated on 26/Apr/22
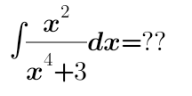
Answered by Mathspace last updated on 26/Apr/22
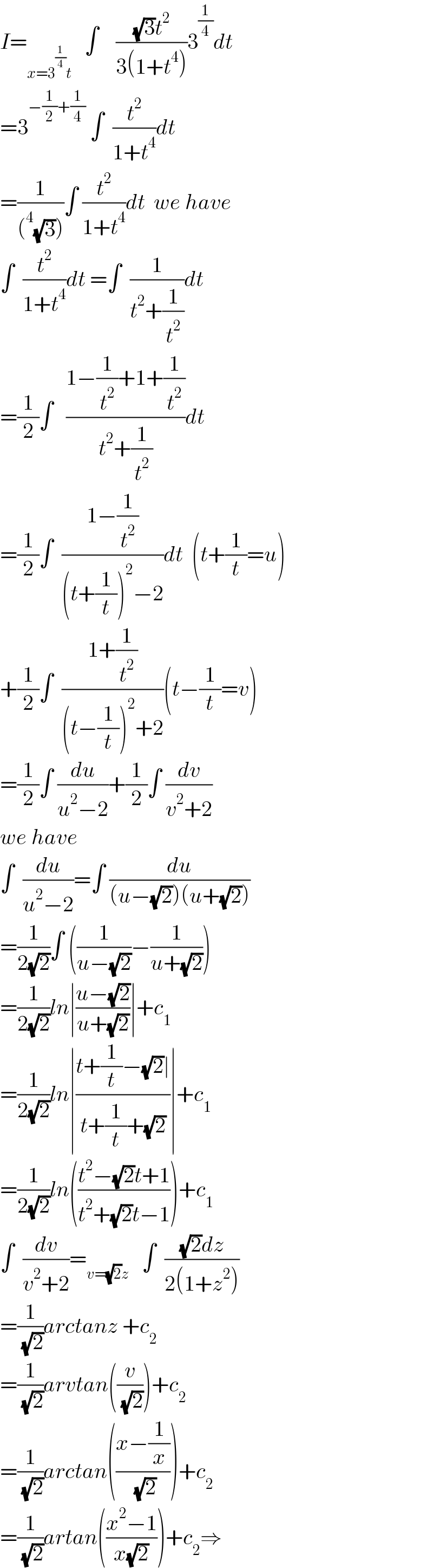
I=_(x=3^(1/4) t) ∫ (((√3)t^2 )/(3(1+t^4 )))3^(1/4) dt =3^(−(1/2)+(1/4)) ∫ (t^2 /(1+t^4 ))dt =(1/((^4 (√3))))∫ (t^2 /(1+t^4 ))dt we have ∫ (t^2 /(1+t^4 ))dt =∫ (1/(t^2 +(1/t^2 )))dt =(1/2)∫ ((1−(1/t^2 )+1+(1/t^2 ))/(t^2 +(1/t^2 )))dt =(1/2)∫ ((1−(1/t^2 ))/((t+(1/t))^2 −2))dt (t+(1/t)=u) +(1/2)∫ ((1+(1/t^2 ))/((t−(1/t))^2 +2))(t−(1/t)=v) =(1/2)∫ (du/(u^2 −2))+(1/2)∫ (dv/(v^2 +2)) we have ∫ (du/(u^2 −2))=∫ (du/((u−(√2))(u+(√2)))) =(1/(2(√2)))∫ ((1/(u−(√2)))−(1/(u+(√2)))) =(1/(2(√2)))ln∣((u−(√2))/(u+(√2)))∣+c_1 =(1/(2(√2)))ln∣((t+(1/t)−(√2)∣)/(t+(1/t)+(√2)))∣+c_1 =(1/(2(√2)))ln(((t^2 −(√2)t+1)/(t^2 +(√2)t−1)))+c_1 ∫ (dv/(v^2 +2))=_(v=(√2)z) ∫ (((√2)dz)/(2(1+z^2 ))) =(1/( (√2)))arctanz +c_2 =(1/( (√2)))arvtan((v/( (√2))))+c_2 =(1/( (√2)))arctan(((x−(1/x))/( (√2))))+c_2 =(1/( (√2)))artan(((x^2 −1)/(x(√2))))+c_2 ⇒
$${I}=_{{x}=\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{4}}} {t}} \:\:\:\int\:\:\:\:\frac{\sqrt{\mathrm{3}}{t}^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{4}}} {dt} \\ $$$$=\mathrm{3}^{−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}} \:\int\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\left(^{\mathrm{4}} \sqrt{\mathrm{3}}\right)}\int\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt}\:\:{we}\:{have} \\ $$$$\int\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt}\:=\int\:\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\mathrm{2}}{dt}\:\:\left({t}+\frac{\mathrm{1}}{{t}}={u}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}}\left({t}−\frac{\mathrm{1}}{{t}}={v}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{dv}}{{v}^{\mathrm{2}} +\mathrm{2}} \\ $$$${we}\:{have} \\ $$$$\int\:\:\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{2}}=\int\:\frac{{du}}{\left({u}−\sqrt{\mathrm{2}}\right)\left({u}+\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\:\left(\frac{\mathrm{1}}{{u}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{u}+\sqrt{\mathrm{2}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\frac{{u}−\sqrt{\mathrm{2}}}{{u}+\sqrt{\mathrm{2}}}\mid+{c}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\frac{{t}+\frac{\mathrm{1}}{{t}}−\sqrt{\mathrm{2}}\mid}{{t}+\frac{\mathrm{1}}{{t}}+\sqrt{\mathrm{2}}}\mid+{c}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}−\mathrm{1}}\right)+{c}_{\mathrm{1}} \\ $$$$\int\:\:\frac{{dv}}{{v}^{\mathrm{2}} +\mathrm{2}}=_{{v}=\sqrt{\mathrm{2}}{z}} \:\:\:\int\:\:\frac{\sqrt{\mathrm{2}}{dz}}{\mathrm{2}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{arctanz}\:+{c}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{arvtan}\left(\frac{{v}}{\:\sqrt{\mathrm{2}}}\right)+{c}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{arctan}\left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)+{c}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{artan}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}\sqrt{\mathrm{2}}}\right)+{c}_{\mathrm{2}} \Rightarrow \\ $$
Commented by Mathspace last updated on 26/Apr/22
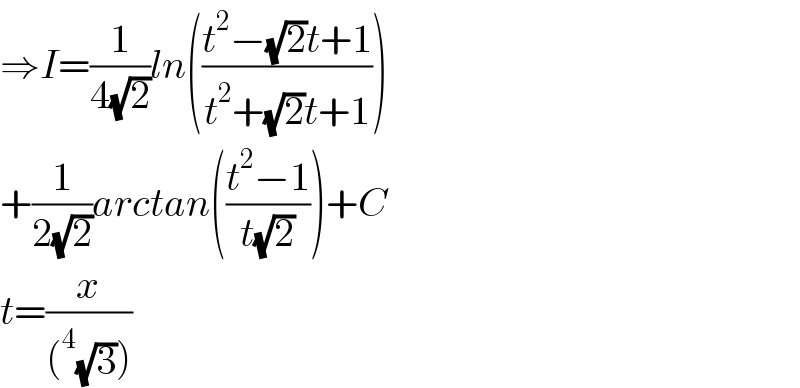
⇒I=(1/(4(√2)))ln(((t^2 −(√2)t+1)/(t^2 +(√2)t+1))) +(1/(2(√2)))arctan(((t^2 −1)/(t(√2))))+C t=(x/((^4 (√3))))
$$\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{arctan}\left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}\sqrt{\mathrm{2}}}\right)+{C} \\ $$$${t}=\frac{{x}}{\left(^{\mathrm{4}} \sqrt{\mathrm{3}}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *