Question Number 169239 by mr W last updated on 26/Apr/22
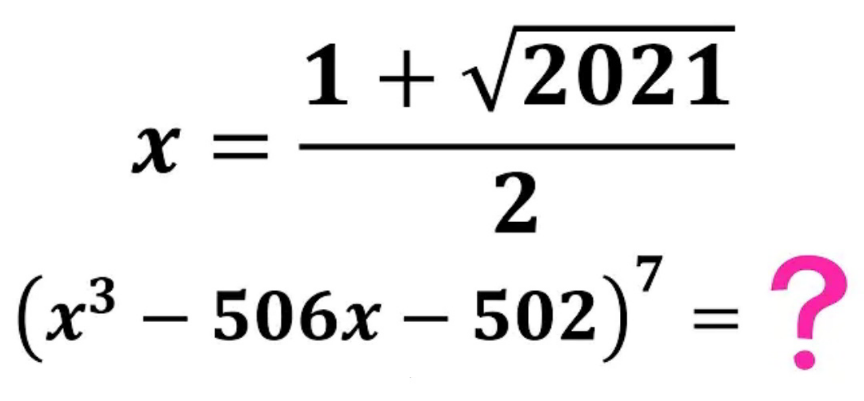
Commented by infinityaction last updated on 26/Apr/22

$$\mathrm{2187}\:??? \\ $$
Commented by infinityaction last updated on 26/Apr/22
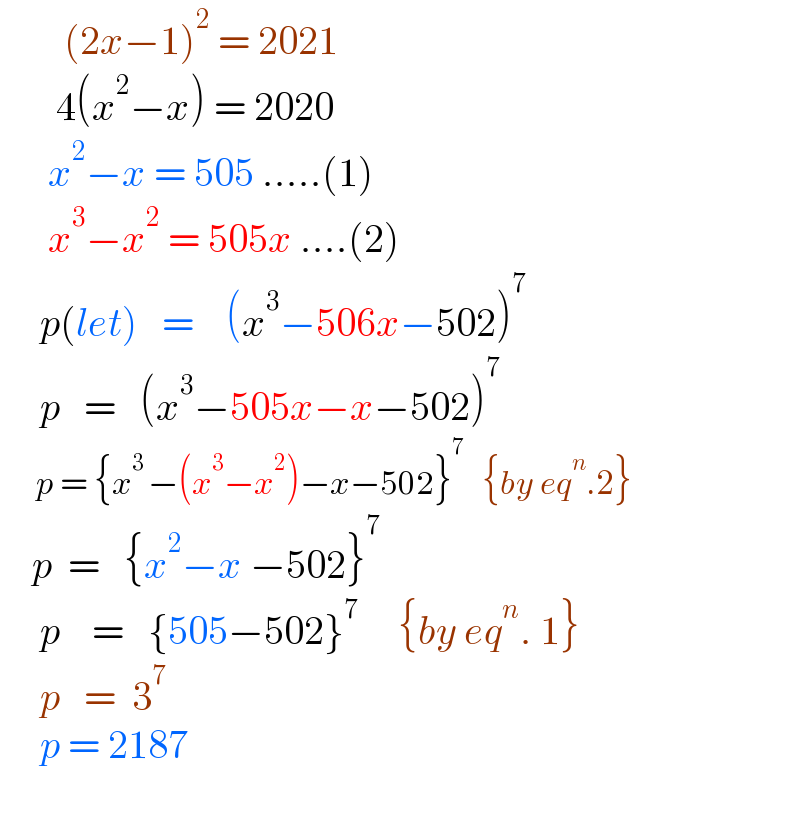
$$\:\:\:\:\:\:\:\:\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2021} \\ $$$$\:\:\:\:\:\:\:\mathrm{4}\left({x}^{\mathrm{2}} −{x}\right)\:=\:\mathrm{2020} \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} −{x}\:=\:\mathrm{505}\:…..\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{3}} −{x}^{\mathrm{2}} \:=\:\mathrm{505}{x}\:….\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:{p}\left({let}\right)\:\:\:=\:\:\:\:\left({x}^{\mathrm{3}} −\mathrm{506}{x}−\mathrm{502}\right)^{\mathrm{7}} \\ $$$$\:\:\:\:\:{p}\:\:\:=\:\:\:\left({x}^{\mathrm{3}} −\mathrm{505}{x}−{x}−\mathrm{502}\right)^{\mathrm{7}} \:\: \\ $$$$\:\:\:\:\:\:{p}\:=\:\left\{{x}^{\mathrm{3}\:} −\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} \right)−{x}−\mathrm{502}\right\}^{\mathrm{7}} \:\:\:\left\{{by}\:{eq}^{{n}} .\mathrm{2}\right\} \\ $$$$\:\:\:\:{p}\:\:=\:\:\:\left\{{x}^{\mathrm{2}} −{x}\:−\mathrm{502}\right\}^{\mathrm{7}} \\ $$$$\:\:\:\:\:{p}\:\:\:\:=\:\:\:\left\{\mathrm{505}−\mathrm{502}\right\}^{\mathrm{7}} \:\:\:\:\:\left\{{by}\:{eq}^{{n}} .\:\mathrm{1}\right\} \\ $$$$\:\:\:\:\:{p}\:\:\:=\:\:\mathrm{3}^{\mathrm{7}} \\ $$$$\:\:\:\:\:{p}\:=\:\mathrm{2187} \\ $$$$ \\ $$
Commented by mr W last updated on 26/Apr/22
��
Commented by Rasheed.Sindhi last updated on 27/Apr/22

$$\vee.\:\:\cap\mathrm{i}\subset\in! \\ $$
Answered by Rasheed.Sindhi last updated on 28/Apr/22

$$\begin{array}{|c|}{\mathbb{A}\mathrm{n}\mathbb{O}\mathrm{ther}\:\mathbb{W}\mathrm{ay}:}\\\hline\end{array} \\ $$$$\underline{{x}=\frac{\mathrm{1}+\sqrt{\mathrm{2021}}}{\mathrm{2}}\:;\:\left({x}^{\mathrm{3}} −\mathrm{506}{x}−\mathrm{502}\right)^{\mathrm{7}} =?} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{506}{x}−\mathrm{502}\right)^{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:=\left({x}^{\mathrm{3}} −\mathrm{506}{x}−\mathrm{505}+\mathrm{3}\right)^{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:=\left\{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}−\mathrm{505}\right)+\mathrm{3}\right\}^{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:=\left\{\left({x}+\mathrm{1}\right)\left(\:{x}\left({x}−\mathrm{1}\right)−\mathrm{505}\:\:\right)+\mathrm{3}\right\}^{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}+\mathrm{1}=\frac{\mathrm{1}+\sqrt{\mathrm{2021}}}{\mathrm{2}}+\mathrm{1}=\frac{\mathrm{3}+\sqrt{\mathrm{2021}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}−\mathrm{1}=\frac{\mathrm{1}+\sqrt{\mathrm{2021}}}{\mathrm{2}}−\mathrm{1}=\frac{−\mathrm{1}+\sqrt{\mathrm{2021}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{2021}}}{\mathrm{2}} \\ $$$$=\left\{\frac{\mathrm{3}+\sqrt{\mathrm{2021}}}{\mathrm{2}}\centerdot\left(\:\frac{\mathrm{1}+\sqrt{\mathrm{2021}}}{\mathrm{2}}\centerdot\frac{−\mathrm{1}+\sqrt{\mathrm{2021}}}{\mathrm{2}}−\mathrm{505}\right)+\mathrm{3}\right\}^{\mathrm{7}} \\ $$$$=\left\{\frac{\mathrm{3}+\sqrt{\mathrm{2021}}}{\mathrm{2}}\centerdot\left(\:\frac{\mathrm{2021}−\mathrm{1}}{\mathrm{4}}−\mathrm{505}\right)+\mathrm{3}\right\}^{\mathrm{7}} \\ $$$$=\left\{\frac{\mathrm{3}+\sqrt{\mathrm{2021}}}{\mathrm{2}}\centerdot\left(\:\mathrm{505}−\mathrm{505}\right)+\mathrm{3}\right\}^{\mathrm{7}} \\ $$$$=\left\{\frac{\mathrm{3}+\sqrt{\mathrm{2021}}}{\mathrm{2}}\left(\mathrm{0}\right)+\mathrm{3}\right\}^{\mathrm{7}} \\ $$$$=\mathrm{3}^{\mathrm{7}} =\mathrm{2187} \\ $$
