Question Number 169272 by cortano1 last updated on 27/Apr/22

Commented by greougoury555 last updated on 27/Apr/22

$$\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by infinityaction last updated on 27/Apr/22
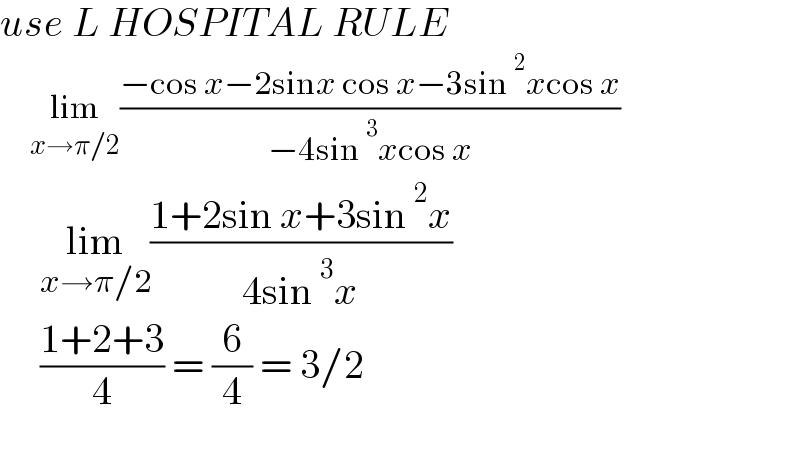
$${use}\:{L}\:{HOSPITAL}\:{RULE} \\ $$$$\:\:\:\:\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\frac{−\mathrm{cos}\:{x}−\mathrm{2sin}{x}\:\mathrm{cos}\:{x}−\mathrm{3sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:{x}}{−\mathrm{4sin}\:^{\mathrm{3}} {x}\mathrm{cos}\:{x}} \\ $$$$\:\:\:\:\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{1}+\mathrm{2sin}\:{x}+\mathrm{3sin}\:^{\mathrm{2}} {x}}{\mathrm{4sin}\:^{\mathrm{3}} {x}} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}+\mathrm{2}+\mathrm{3}}{\mathrm{4}}\:=\:\frac{\mathrm{6}}{\mathrm{4}}\:=\:\mathrm{3}/\mathrm{2} \\ $$$$ \\ $$
Commented by greougoury555 last updated on 28/Apr/22
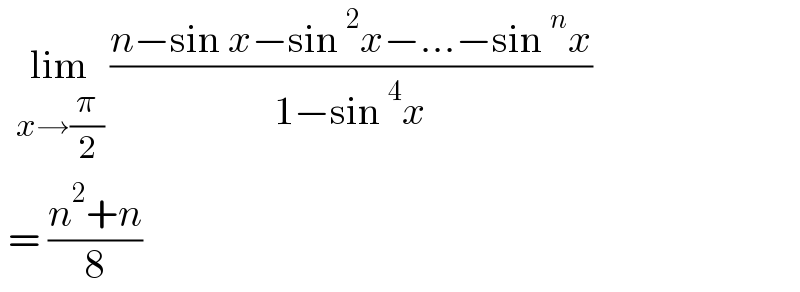
$$\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{{n}−\mathrm{sin}\:{x}−\mathrm{sin}\:^{\mathrm{2}} {x}−…−\mathrm{sin}\:^{{n}} {x}}{\mathrm{1}−\mathrm{sin}\:^{\mathrm{4}} {x}} \\ $$$$\:=\:\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{8}} \\ $$
