Question Number 169281 by mnjuly1970 last updated on 28/Apr/22
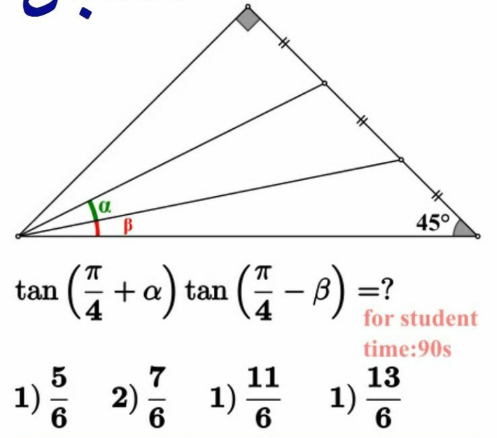
Commented by cortano1 last updated on 28/Apr/22
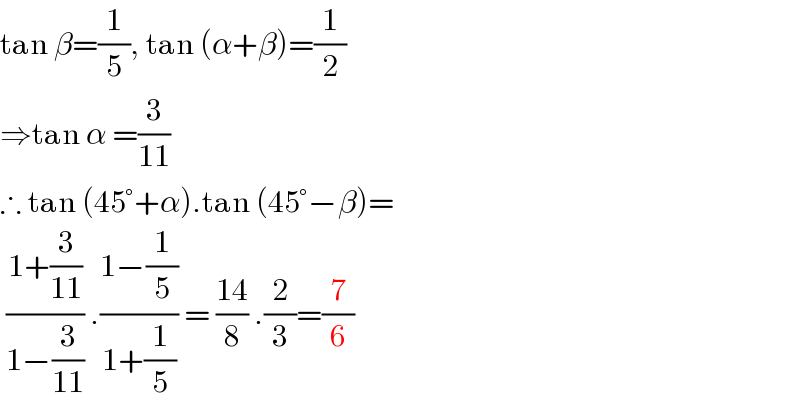
$$\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{5}},\:\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha\:=\frac{\mathrm{3}}{\mathrm{11}} \\ $$$$\therefore\:\mathrm{tan}\:\left(\mathrm{45}°+\alpha\right).\mathrm{tan}\:\left(\mathrm{45}°−\beta\right)= \\ $$$$\:\frac{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{11}}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{11}}}\:.\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}}\:=\:\frac{\mathrm{14}}{\mathrm{8}}\:.\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{6}} \\ $$
Commented by mnjuly1970 last updated on 28/Apr/22

$${mercey}\:{mr}\:{cartano} \\ $$
