Question Number 169294 by cortano1 last updated on 28/Apr/22

Commented by qaz last updated on 28/Apr/22
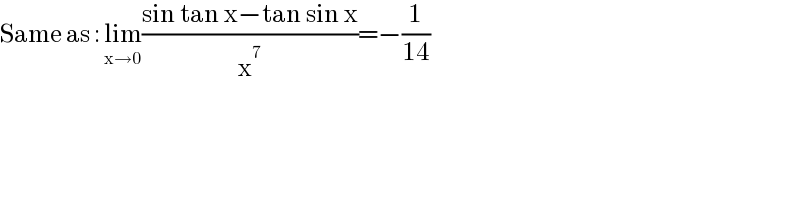
$$\mathrm{Same}\:\mathrm{as}\::\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{tan}\:\mathrm{x}−\mathrm{tan}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{7}} }=−\frac{\mathrm{1}}{\mathrm{14}} \\ $$
Commented by cortano1 last updated on 28/Apr/22

$${your}\:{answer}\:{wrong} \\ $$
Answered by bobhans last updated on 28/Apr/22
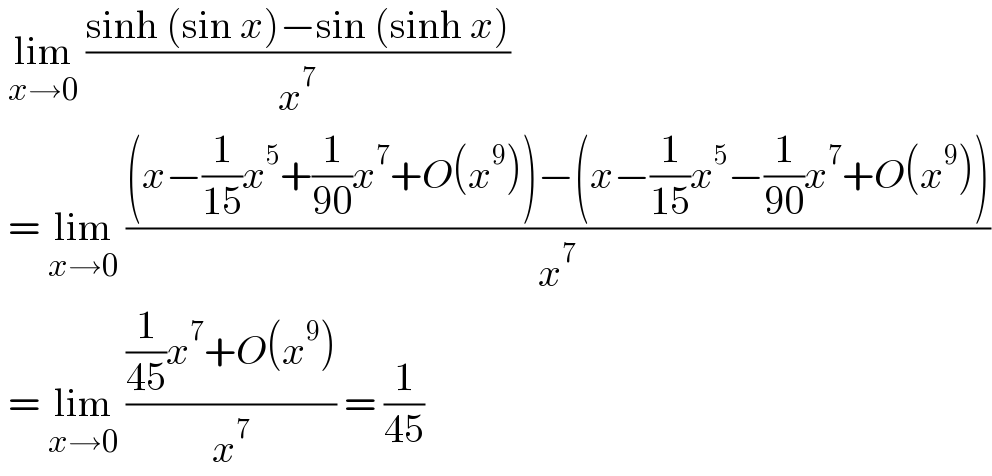
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sinh}\:\left(\mathrm{sin}\:{x}\right)−\mathrm{sin}\:\left(\mathrm{sinh}\:{x}\right)}{{x}^{\mathrm{7}} }\: \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({x}−\frac{\mathrm{1}}{\mathrm{15}}{x}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{90}}{x}^{\mathrm{7}} +{O}\left({x}^{\mathrm{9}} \right)\right)−\left({x}−\frac{\mathrm{1}}{\mathrm{15}}{x}^{\mathrm{5}} −\frac{\mathrm{1}}{\mathrm{90}}{x}^{\mathrm{7}} +{O}\left({x}^{\mathrm{9}} \right)\right)}{{x}^{\mathrm{7}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{45}}{x}^{\mathrm{7}} +{O}\left({x}^{\mathrm{9}} \right)}{{x}^{\mathrm{7}} }\:=\:\frac{\mathrm{1}}{\mathrm{45}} \\ $$
